Question and Answers Forum

AlgebraQuestion and Answers: Page 223

Question Number 132900 Answers: 0 Comments: 1

a pinhole camera is placed 300cm in front of a building so that the image is formed on a screen 5cm from the pin hole. if the image is 2.5cm high. the height of the building will be?

$${a}\:{pinhole}\:{camera}\:{is}\:{placed}\:\mathrm{300}{cm} \\ $$$${in}\:{front}\:{of}\:{a}\:{building}\:{so}\:{that}\:{the}\:{image} \\ $$$${is}\:{formed}\:{on}\:{a}\:{screen}\:\mathrm{5}{cm}\:{from}\:{the} \\ $$$${pin}\:{hole}.\:{if}\:{the}\:{image}\:{is}\:\mathrm{2}.\mathrm{5}{cm}\:{high}. \\ $$$${the}\:{height}\:{of}\:{the}\:{building}\:{will}\:{be}? \\ $$

Question Number 132697 Answers: 3 Comments: 2

Find the condition that one root of ax^2 +bx+c = 0 ,a≠ 0 is square of the other .

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{that}\:\mathrm{one} \\ $$$$\mathrm{root}\:\mathrm{of}\:{ax}^{\mathrm{2}} +{bx}+{c}\:=\:\mathrm{0}\:,{a}\neq\:\mathrm{0} \\ $$$$\mathrm{is}\:\mathrm{square}\:\mathrm{of}\:\mathrm{the}\:\mathrm{other}\:. \\ $$

Question Number 132630 Answers: 0 Comments: 0

Question Number 132535 Answers: 1 Comments: 0

Question Number 132494 Answers: 2 Comments: 3

Question Number 132470 Answers: 2 Comments: 0

∫ tan^3 x dx

$$\int\:\mathrm{tan}^{\mathrm{3}} {x}\:{dx} \\ $$

Question Number 132390 Answers: 1 Comments: 0

does anyone know a practicaly way of finding results from (4−3x+2x^2 −x^4 )×(−1+3x^2 −x^5 )?

$$\mathrm{does}\:\mathrm{anyone}\:\mathrm{know}\:\mathrm{a}\:\mathrm{practicaly} \\ $$$$\mathrm{way}\:\mathrm{of}\:\mathrm{finding}\:\mathrm{results}\:\mathrm{from} \\ $$$$\:\left(\mathrm{4}−\mathrm{3x}+\mathrm{2x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{4}} \right)×\left(−\mathrm{1}+\mathrm{3x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{5}} \right)? \\ $$

Question Number 132358 Answers: 0 Comments: 2

find the equation whose roots are α and β. find α and β if α−β=2 and α^2 −β^2 =3

$${find}\:{the}\:{equation}\:{whose}\:{roots}\:{are} \\ $$$$\alpha\:{and}\:\beta.\:{find}\:\alpha\:{and}\:\beta\:{if}\:\:\alpha−\beta=\mathrm{2}\:{and}\:\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} =\mathrm{3} \\ $$

Question Number 132295 Answers: 0 Comments: 4

Question Number 132285 Answers: 2 Comments: 0

Simplify the equation of (((x^(1/3) −x^(1/6) )(x^(1/2) +x)(x^(1/2) +x^(1/3) +x^(2/3) ))/((x^(4/3) −x)(x+x^(1/3) +x^(2/3) ))) with x ≠ 0

Question Number 132260 Answers: 1 Comments: 0

Question Number 132257 Answers: 1 Comments: 0

Question Number 132198 Answers: 2 Comments: 0

If { ((16^(a+b) = ((√2)/2))),((16^(b+c) = 2)),((16^(a+c) = 2(√2))) :} then c = __

$$\mathrm{If}\:\begin{cases}{\mathrm{16}^{{a}+{b}} \:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\\{\mathrm{16}^{{b}+{c}} \:=\:\mathrm{2}}\\{\mathrm{16}^{{a}+{c}} \:=\:\mathrm{2}\sqrt{\mathrm{2}}}\end{cases} \\ $$$$\:\mathrm{then}\:\mathrm{c}\:=\:\_\_\: \\ $$

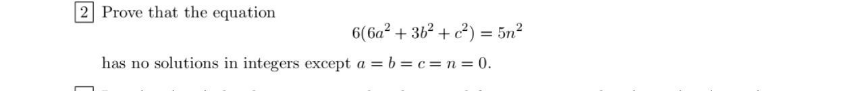
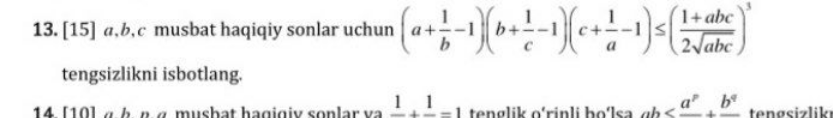
Question Number 132180 Answers: 1 Comments: 0

solve : 2sec^2 x+(2(√2)−3)secx−3(√2)=0 ; 0≤x≤(π/4)

$${solve}\:: \\ $$$$\mathrm{2}{sec}^{\mathrm{2}} {x}+\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3}\right){secx}−\mathrm{3}\sqrt{\mathrm{2}}=\mathrm{0}\:;\:\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{4}} \\ $$

Question Number 132031 Answers: 0 Comments: 3

Question Number 131932 Answers: 1 Comments: 0

if x=18 and y=17 then find (x+y)(x^2 +y^2 )(x^4 +y^4 )(x^8 +y^8 )

$${if}\:{x}=\mathrm{18}\:{and}\:{y}=\mathrm{17}\:{then}\:{find} \\ $$$$\left({x}+{y}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{4}} +{y}^{\mathrm{4}} \right)\left({x}^{\mathrm{8}} +{y}^{\mathrm{8}} \right) \\ $$

Question Number 131697 Answers: 2 Comments: 0

x^x =6 x=?

$${x}^{{x}} =\mathrm{6}\:\:\:\:\:\:\:\:\:\:{x}=? \\ $$

Question Number 131688 Answers: 2 Comments: 0

Let α and β are the roots of the equation x^2 −6x−2=0. If a_n = α^n −β^n for n ≥1 then the value of ((a_(10) −2a_8 )/(2a_9 )) ?

$$\:\mathrm{Let}\:\alpha\:\mathrm{and}\:\beta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\: \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{x}^{\mathrm{2}} −\mathrm{6x}−\mathrm{2}=\mathrm{0}. \\ $$$$\mathrm{If}\:{a}_{{n}} \:=\:\alpha^{{n}} −\beta^{{n}} \:\mathrm{for}\:{n}\:\geqslant\mathrm{1}\: \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\frac{{a}_{\mathrm{10}} −\mathrm{2}{a}_{\mathrm{8}} }{\mathrm{2}{a}_{\mathrm{9}} }\:? \\ $$

Question Number 131640 Answers: 1 Comments: 0

Question Number 131605 Answers: 2 Comments: 0

solve the equation m^4 −7m^3 + 14m^2 −7m + 1 = 0

$$\mathrm{solve}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\:\:{m}^{\mathrm{4}} −\mathrm{7}{m}^{\mathrm{3}} +\:\mathrm{14}{m}^{\mathrm{2}} −\mathrm{7}{m}\:+\:\mathrm{1}\:=\:\mathrm{0}\: \\ $$

Question Number 131480 Answers: 0 Comments: 0

what are the condition for absolute inequality?

$${what}\:{are}\:{the}\:{condition}\:{for}\:{absolute}\: \\ $$$${inequality}? \\ $$

Question Number 131440 Answers: 0 Comments: 2

∣2x+7∣<−2 solve=?

$$\mid\mathrm{2}{x}+\mathrm{7}\mid<−\mathrm{2}\:\:\:\:\:\:{solve}=? \\ $$

Question Number 131430 Answers: 2 Comments: 2

(((((x^x )^x ))^(1/(1/x)) ))^(1/(1/x)) =4 find x=?

$$\sqrt[{\frac{\mathrm{1}}{{x}}}]{\left(\sqrt[{\frac{\mathrm{1}}{{x}}}]{\left.{x}\:^{{x}} \right)^{{x}} }\right.}=\mathrm{4}\:\:\:\:\:\:\:{find}\:\:{x}=? \\ $$

Question Number 131421 Answers: 0 Comments: 1

Solve using trig method 8x^3 −4x^2 −4x+1=0

$$\mathrm{Solve}\:\mathrm{using}\:\mathrm{trig}\:\mathrm{method} \\ $$$$\:\:\mathrm{8x}^{\mathrm{3}} −\mathrm{4x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{1}=\mathrm{0} \\ $$

Question Number 131390 Answers: 0 Comments: 0

Question Number 131374 Answers: 3 Comments: 0

Pg 218 Pg 219 Pg 220 Pg 221 Pg 222 Pg 223 Pg 224 Pg 225 Pg 226 Pg 227

Contact: info@tinkutara.com