Question and Answers Forum

AlgebraQuestion and Answers: Page 222

Question Number 135486 Answers: 4 Comments: 3

(((√(2x+1))+(√(x−1)))/( (√(2x+1))−(√(x−1)))) = (3/( (√(x+2))))

$$\frac{\sqrt{\mathrm{2x}+\mathrm{1}}+\sqrt{\mathrm{x}−\mathrm{1}}}{\:\sqrt{\mathrm{2x}+\mathrm{1}}−\sqrt{\mathrm{x}−\mathrm{1}}}\:=\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{x}+\mathrm{2}}}\: \\ $$

Question Number 135472 Answers: 1 Comments: 0

for x+y+z=10 with x,y,z∈N find Σ((10!)/(x!y!z!))

$${for}\:{x}+{y}+{z}=\mathrm{10}\:{with}\:{x},{y},{z}\in\mathbb{N} \\ $$$${find}\:\Sigma\frac{\mathrm{10}!}{{x}!{y}!{z}!} \\ $$

Question Number 135424 Answers: 1 Comments: 0

Find solution set the inequality (√(2x−5)) + (√(25−3x)) > x

$${Find}\:{solution}\:{set}\:{the}\:{inequality} \\ $$$$\sqrt{\mathrm{2}{x}−\mathrm{5}}\:+\:\sqrt{\mathrm{25}−\mathrm{3}{x}}\:>\:{x} \\ $$

Question Number 135420 Answers: 1 Comments: 0

Algebra Pipe A can fill a tank in two hours and pipe B can fill it in half the time it takes pipe C to empty it. When all 3 are opened, it takes 1.5 hours to fill the pool how much time is required for pipe 'C to empty the tank?

$${Algebra} \\ $$Pipe A can fill a tank in two hours and pipe B can fill it in half the time it takes pipe C to empty it. When all 3 are opened, it takes 1.5 hours to fill the pool how much time is required for pipe 'C to empty the tank?

Question Number 135418 Answers: 2 Comments: 0

Given x+(1/x) = 5 then ((x^4 +(1/x^4 ))/(x^2 −3x+1)) ?

$${Given}\:{x}+\frac{\mathrm{1}}{{x}}\:=\:\mathrm{5}\:{then}\:\frac{{x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{1}}\:? \\ $$

Question Number 135415 Answers: 3 Comments: 1

Question Number 135413 Answers: 0 Comments: 1

Question Number 135364 Answers: 0 Comments: 0

Question Number 135354 Answers: 1 Comments: 0

Algebra A & B together can finish a work in 24 days, B & C in 30 days. If C is 20% more efficient than B, then how many days are required for A alone to finish the work?

$${Algebra} \\ $$A & B together can finish a work in 24 days, B & C in 30 days. If C is 20% more efficient than B, then how many days are required for A alone to finish the work?

Question Number 135305 Answers: 1 Comments: 0

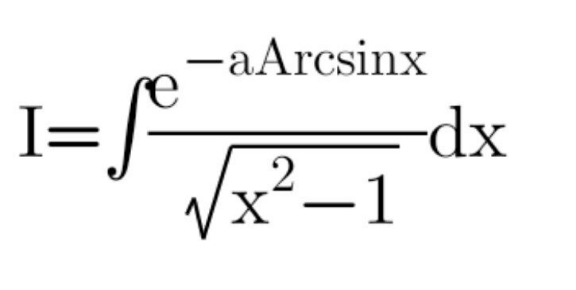
Question Number 135300 Answers: 3 Comments: 0

((√2) +(√3) +1)((√2) −(√3) +1)((√2) +(√3)−1)((√2)−(√3)−1)=?

$$\left(\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}\:+\mathrm{1}\right)\left(\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{3}}\:+\mathrm{1}\right)\left(\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}−\mathrm{1}\right)\left(\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}−\mathrm{1}\right)=? \\ $$

Question Number 135298 Answers: 2 Comments: 0

Question Number 135285 Answers: 1 Comments: 0

pre−calculus if log_(48) ^(72) +log_(54) ^(12) =k then log_( 12) ^( 27) =???

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{pre}−{calculus} \\ $$$$\:\:{if}\:\:\:\:\:\:\:{log}_{\mathrm{48}} ^{\mathrm{72}} +{log}_{\mathrm{54}} ^{\mathrm{12}} \:={k}\: \\ $$$$\:\:\:\:\:\:{then}\:\:{log}_{\:\mathrm{12}} ^{\:\mathrm{27}} \:\:=??? \\ $$$$\:\:\:\:\:\:\:\: \\ $$

Question Number 135230 Answers: 0 Comments: 0

A hockey team plays in an arena that has a seating capacity of 15,000 spectators. With the ticket price seat at $14, average attendance at recent games has been 9500. A market survey indicates that for each dollar the ticket price is lowered ,the average attendance increases by 1000. (a) Find a function that models the revenue in terms of ticket price (b) Find the price that maximizes revenue from ticket sales (c) What ticket price is so high that no one attends and so no is generated

$${A}\:{hockey}\:{team}\:{plays}\:{in}\:{an}\:{arena}\:{that} \\ $$$${has}\:{a}\:{seating}\:{capacity}\:{of}\:\mathrm{15},\mathrm{000} \\ $$$${spectators}.\:{With}\:{the}\:{ticket}\:{price} \\ $$$${seat}\:{at}\:\$\mathrm{14},\:{average}\:{attendance} \\ $$$${at}\:{recent}\:{games}\:{has}\:{been}\:\mathrm{9500}. \\ $$$${A}\:{market}\:{survey}\:{indicates}\:{that} \\ $$$${for}\:{each}\:{dollar}\:{the}\:{ticket}\:{price} \\ $$$${is}\:{lowered}\:,{the}\:{average}\:{attendance} \\ $$$${increases}\:{by}\:\mathrm{1000}. \\ $$$$\left(\boldsymbol{{a}}\right)\:\boldsymbol{{F}}{ind}\:{a}\:{function}\:{that}\:{models} \\ $$$${the}\:{revenue}\:{in}\:{terms}\:{of}\:{ticket} \\ $$$${price} \\ $$$$\left({b}\right)\:{Find}\:{the}\:{price}\:{that}\:{maximizes} \\ $$$${revenue}\:{from}\:{ticket}\:{sales} \\ $$$$\left({c}\right)\:{What}\:{ticket}\:{price}\:{is}\:{so}\:{high} \\ $$$${that}\:{no}\:{one}\:{attends}\:{and}\:{so}\:{no} \\ $$$${is}\:{generated} \\ $$

Question Number 135191 Answers: 2 Comments: 0

{ ((x^2 −yz = 3)),((y^2 − zx = 5)),((z^2 −xy = −1)) :} solve for x ,y and z.

$$\begin{cases}{\mathrm{x}^{\mathrm{2}} −\mathrm{yz}\:=\:\mathrm{3}}\\{\mathrm{y}^{\mathrm{2}} −\:\mathrm{zx}\:=\:\mathrm{5}}\\{\mathrm{z}^{\mathrm{2}} −\mathrm{xy}\:=\:−\mathrm{1}}\end{cases} \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{x}\:,\mathrm{y}\:\mathrm{and}\:\mathrm{z}. \\ $$

Question Number 135172 Answers: 2 Comments: 0

(x^2 −9)^(3x+5) = (x−3)^(x−1) .(x+3)^(x−1) Find solution

$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{3x}+\mathrm{5}} \:=\:\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{x}−\mathrm{1}} .\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{x}−\mathrm{1}} \\ $$$$\mathrm{Find}\:\mathrm{solution} \\ $$

Question Number 135170 Answers: 1 Comments: 0

1+(2/3)+(3/3^2 )+(4/3^3 )+(5/3^4 )+(6/3^5 )+... =?

$$\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{3}^{\mathrm{4}} }+\frac{\mathrm{6}}{\mathrm{3}^{\mathrm{5}} }+...\:=?\: \\ $$$$ \\ $$

Question Number 135121 Answers: 0 Comments: 0