Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 203964 by mnjuly1970 last updated on 03/Feb/24

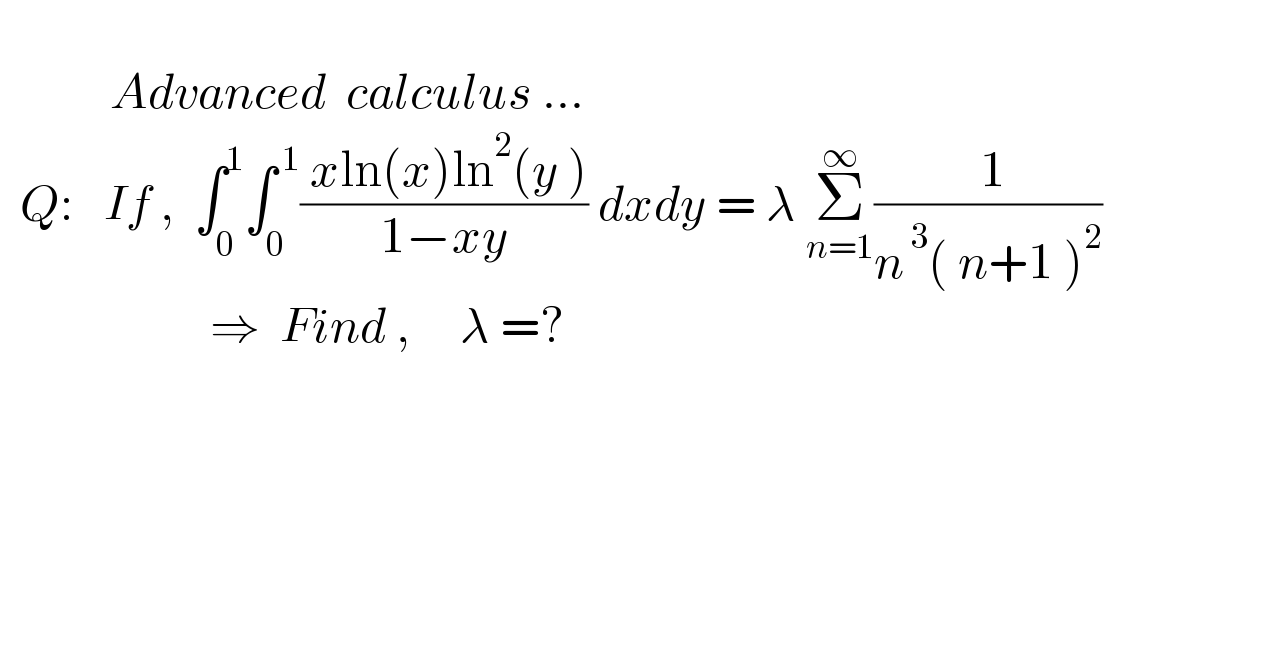
Advanced calculus ... Q: If , ∫_0 ^1 ∫_0 ^( 1) (( xln(x)ln^2 (y ))/(1−xy)) dxdy = λ Σ_(n=1) ^∞ (( 1)/(n^( 3) ( n+1 )^2 )) ⇒ Find , λ =?

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{Advanced}\:\:{calculus}\:... \\ $$$$\:\:{Q}:\:\:\:{If}\:,\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{x}\mathrm{ln}\left({x}\right)\mathrm{ln}^{\mathrm{2}} \left({y}\:\right)}{\mathrm{1}−{xy}}\:{dxdy}\:=\:\lambda\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\mathrm{1}}{{n}^{\:\mathrm{3}} \left(\:{n}+\mathrm{1}\:\right)^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:{Find}\:,\:\:\:\:\:\lambda\:=? \\ $$$$ \\ $$

Answered by witcher3 last updated on 03/Feb/24

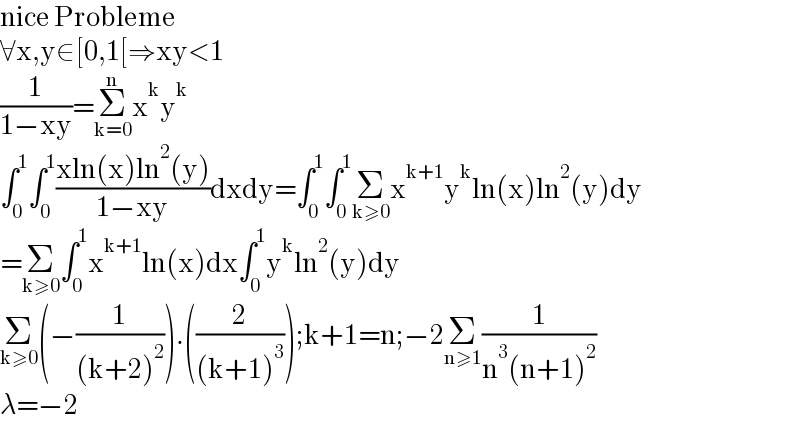
nice Probleme ∀x,y∈[0,1[⇒xy<1 (1/(1−xy))=Σ_(k=0) ^n x^k y^k ∫_0 ^1 ∫_0 ^1 ((xln(x)ln^2 (y))/(1−xy))dxdy=∫_0 ^1 ∫_0 ^1 Σ_(k≥0) x^(k+1) y^k ln(x)ln^2 (y)dy =Σ_(k≥0) ∫_0 ^1 x^(k+1) ln(x)dx∫_0 ^1 y^k ln^2 (y)dy Σ_(k≥0) (−(1/((k+2)^2 ))).((2/((k+1)^3 )));k+1=n;−2Σ_(n≥1) (1/(n^3 (n+1)^2 )) λ=−2

$$\mathrm{nice}\:\mathrm{Probleme} \\ $$$$\forall\mathrm{x},\mathrm{y}\in\left[\mathrm{0},\mathrm{1}\left[\Rightarrow\mathrm{xy}<\mathrm{1}\right.\right. \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−\mathrm{xy}}=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{x}^{\mathrm{k}} \mathrm{y}^{\mathrm{k}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{xln}\left(\mathrm{x}\right)\mathrm{ln}^{\mathrm{2}} \left(\mathrm{y}\right)}{\mathrm{1}−\mathrm{xy}}\mathrm{dxdy}=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\mathrm{x}^{\mathrm{k}+\mathrm{1}} \mathrm{y}^{\mathrm{k}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{ln}^{\mathrm{2}} \left(\mathrm{y}\right)\mathrm{dy} \\ $$$$=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{k}+\mathrm{1}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{y}^{\mathrm{k}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{y}\right)\mathrm{dy} \\ $$$$\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\left(−\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{2}\right)^{\mathrm{2}} }\right).\left(\frac{\mathrm{2}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{3}} }\right);\mathrm{k}+\mathrm{1}=\mathrm{n};−\mathrm{2}\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\lambda=−\mathrm{2} \\ $$

Commented by mnjuly1970 last updated on 03/Feb/24

thanks alot sir wicher

$${thanks}\:\:{alot}\:{sir}\:{wicher} \\ $$

Commented by witcher3 last updated on 04/Feb/24

withe Pleasur

$$\mathrm{withe}\:\mathrm{Pleasur} \\ $$

Answered by MathematicalUser2357 last updated on 06/Feb/24

λ=−2

$$\lambda=−\mathrm{2} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com