
Question Number 140885 by mnjuly1970 last updated on 13/May/21
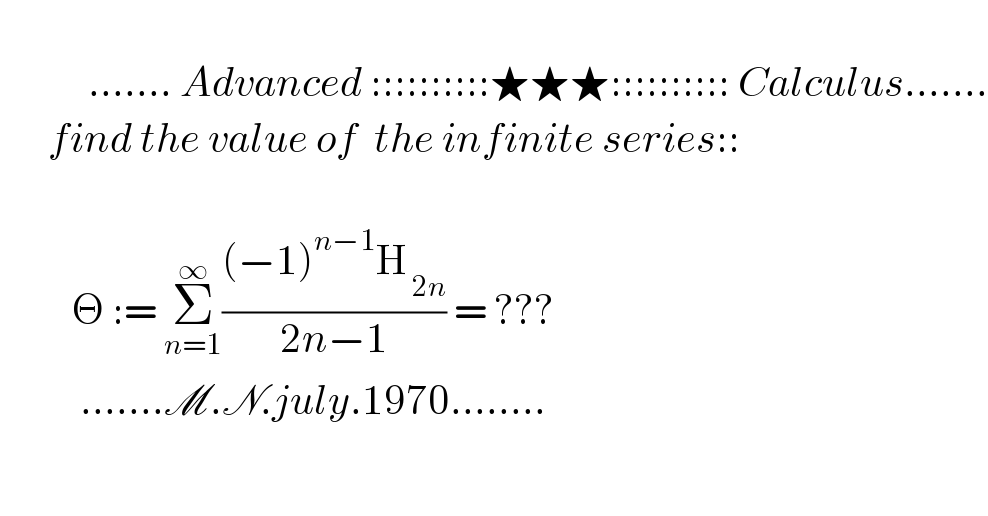
$$\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:.......\:{Advanced}\:::::::::::\bigstar\bigstar\bigstar::::::::::\:{Calculus}....... \\ $$$$\:\:\:\:\:\:{find}\:{the}\:{value}\:{of}\:\:{the}\:{infinite}\:{series}:: \\ $$$$\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\Theta\::=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \mathrm{H}_{\:\mathrm{2}{n}} }{\mathrm{2}{n}−\mathrm{1}}\:=\:??? \\ $$$$\:\:\:\:\:\:\:\:\:\:.......\mathscr{M}.\mathscr{N}.{july}.\mathrm{1970}........ \\ $$
Answered by mindispower last updated on 15/May/21
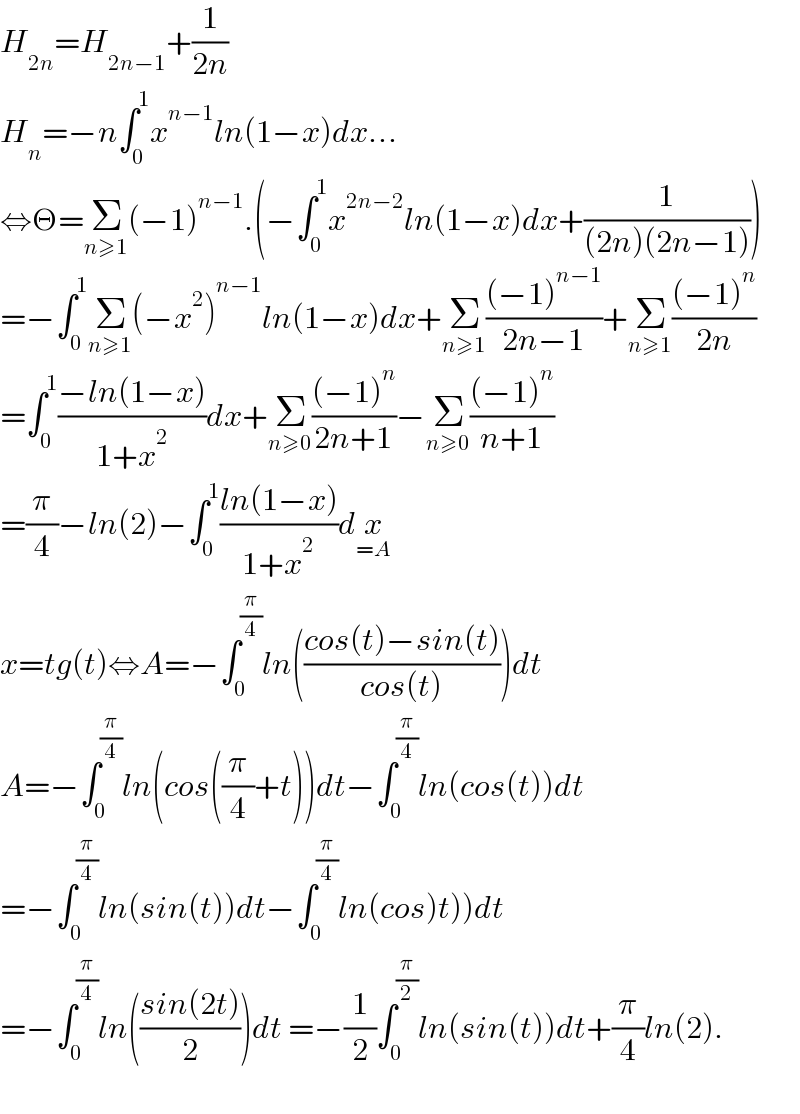
$${H}_{\mathrm{2}{n}} ={H}_{\mathrm{2}{n}−\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$${H}_{{n}} =−{n}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx}... \\ $$$$\Leftrightarrow\Theta=\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} .\left(−\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{n}−\mathrm{2}} {ln}\left(\mathrm{1}−{x}\right){dx}+\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}\right) \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{1}} {\sum}\left(−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}−\mathrm{1}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}+\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}−\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}} \\ $$$$=\frac{\pi}{\mathrm{4}}−{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{d}\underset{={A}} {{x}} \\ $$$${x}={tg}\left({t}\right)\Leftrightarrow{A}=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{{cos}\left({t}\right)−{sin}\left({t}\right)}{{cos}\left({t}\right)}\right){dt} \\ $$$${A}=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\frac{\pi}{\mathrm{4}}+{t}\right)\right){dt}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({t}\right)\right){dt} \\ $$$$\left.=\left.−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sin}\left({t}\right)\right){dt}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\right){t}\right)\right){dt} \\ $$$$=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{{sin}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right){dt}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({t}\right)\right){dt}+\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right). \\ $$$$ \\ $$
