Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 169145 by MathsFan last updated on 24/Apr/22

ABC is a triangle in which the bisector of angle at B meet the side AC at D, and the bisector of the angle BDC is parallel to the side AB. Prove that the △ABC is issoceles triangle.

$$\boldsymbol{{ABC}}\:\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{triangle}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{which}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{bisector}} \\ $$$$\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{angle}}\:\boldsymbol{\mathrm{at}}\:\boldsymbol{{B}}\:\boldsymbol{\mathrm{meet}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{side}}\:\boldsymbol{{AC}}\:\boldsymbol{\mathrm{at}}\:\boldsymbol{{D}}, \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{bisector}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{angle}}\:\boldsymbol{{BDC}}\:\boldsymbol{\mathrm{is}} \\ $$$$\:\boldsymbol{\mathrm{parallel}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{side}}\:\boldsymbol{{AB}}.\:\boldsymbol{\mathrm{Prove}}\:\boldsymbol{\mathrm{that}} \\ $$$$\:\boldsymbol{\mathrm{the}}\:\bigtriangleup\boldsymbol{{ABC}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{issoceles}}\:\boldsymbol{\mathrm{triangle}}. \\ $$$$ \\ $$

Answered by som(math1967) last updated on 25/Apr/22

let bisector of ∠BDC meet the side BC at E ∠ABD=∠DBE=α [BD bisector] ∠ABD=∠BDE [alternate ] ∠BDE=∠EDC=α [DE bisector] AB∥DE ∴ ∠EDC=∠BAC=α AC=b,AB=c, BC=a ∴ (a/(sinα))=(b/(sin2α)) ⇒(a/(sinα))=(b/(2sinαcosα)) ⇒cosα=(b/(2a)) ⇒((b^2 +c^2 −a^2 )/(2bc))=(b/(2a)) ⇒b^2 a+c^2 a−a^3 −b^2 c=0 ⇒b^2 (a−c) −a(a^2 −c^2 )=0 ⇒(a−c)(b^2 −ac−a^2 )=0 a−c=0 ⇒a=c triangle is isoscale

$${let}\:{bisector}\:{of}\:\angle{BDC}\:{meet}\:{the} \\ $$$${side}\:{BC}\:{at}\:{E} \\ $$$$\angle{ABD}=\angle{DBE}=\alpha\:\left[{BD}\:{bisector}\right] \\ $$$$\angle{ABD}=\angle{BDE}\:\left[{alternate}\:\right] \\ $$$$\angle{BDE}=\angle{EDC}=\alpha\:\left[{DE}\:{bisector}\right] \\ $$$${AB}\parallel{DE}\:\therefore\:\angle{EDC}=\angle{BAC}=\alpha \\ $$$$\:{AC}={b},{AB}={c},\:{BC}={a} \\ $$$$\therefore\:\frac{{a}}{{sin}\alpha}=\frac{{b}}{{sin}\mathrm{2}\alpha} \\ $$$$\Rightarrow\frac{{a}}{{sin}\alpha}=\frac{{b}}{\mathrm{2}{sin}\alpha{cos}\alpha} \\ $$$$\Rightarrow{cos}\alpha=\frac{{b}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}=\frac{{b}}{\mathrm{2}{a}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} {a}+{c}^{\mathrm{2}} {a}−{a}^{\mathrm{3}} −{b}^{\mathrm{2}} {c}=\mathrm{0} \\ $$$$\Rightarrow{b}^{\mathrm{2}} \left({a}−{c}\right)\:−{a}\left({a}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\left({a}−{c}\right)\left({b}^{\mathrm{2}} −{ac}−{a}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${a}−{c}=\mathrm{0}\:\Rightarrow{a}={c} \\ $$$${triangle}\:{is}\:{isoscale}\: \\ $$

Commented by som(math1967) last updated on 25/Apr/22

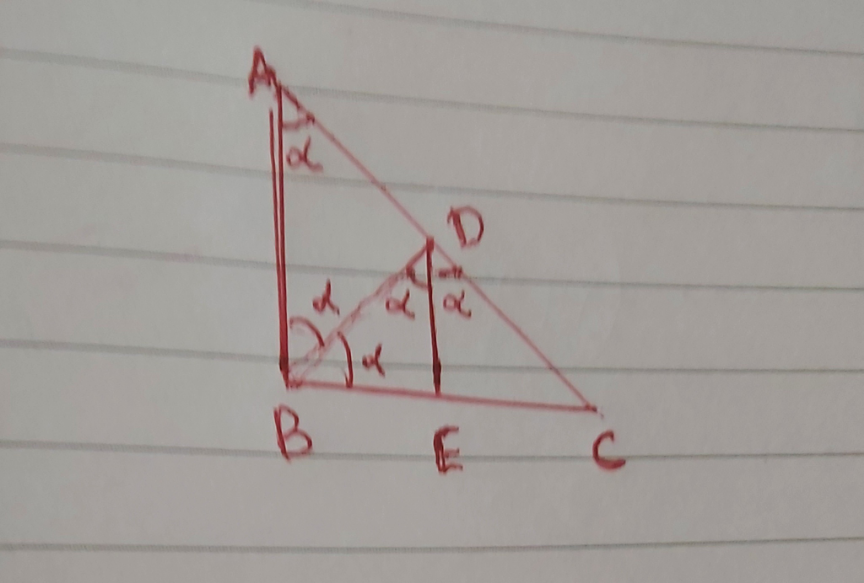
Commented by som(math1967) last updated on 25/Apr/22

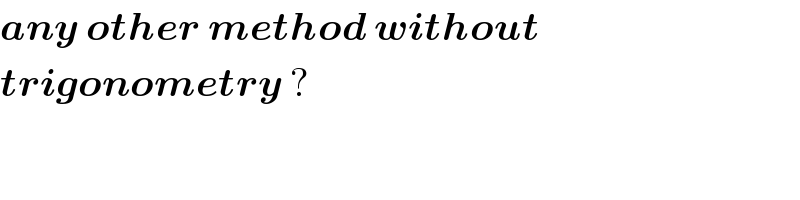
any other method without trigonometry ?

$$\boldsymbol{{any}}\:\boldsymbol{{other}}\:\boldsymbol{{method}}\:\boldsymbol{{without}} \\ $$$$\boldsymbol{{trigonometry}}\:? \\ $$

Commented by MathsFan last updated on 25/Apr/22

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com