Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 213606 by CrispyXYZ last updated on 10/Nov/24

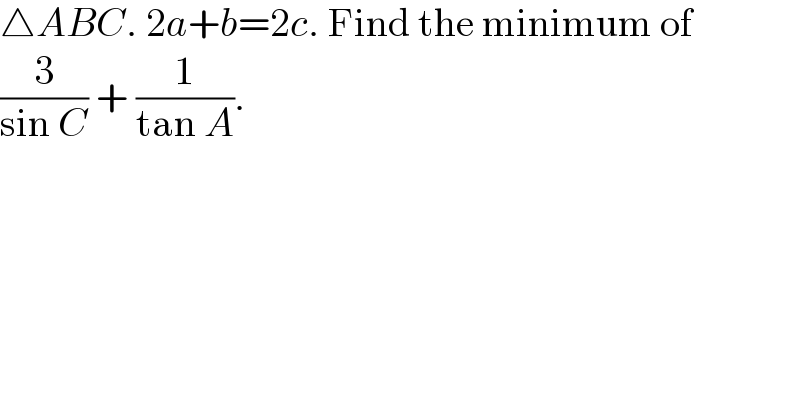
△ABC. 2a+b=2c. Find the minimum of (3/(sin C)) + (1/(tan A)).

$$\bigtriangleup{ABC}.\:\mathrm{2}{a}+{b}=\mathrm{2}{c}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of} \\ $$$$\frac{\mathrm{3}}{\mathrm{sin}\:{C}}\:+\:\frac{\mathrm{1}}{\mathrm{tan}\:{A}}. \\ $$

Answered by Ghisom last updated on 10/Nov/24

wlog b=1 ⇒ c=a+(1/2) a^2 +b^2 −2abcos γ =c^2 b^2 +c^2 −2bccos α =a^2 cos γ =((3−4a)/(8a)) cos α =((4a+5)/(4(2a+1))) (3/(sin γ))+(1/(tan α))=((28a+5)/( (√(3(4a−1)(4a+3))))) ((d[((28a+5)/( (√(3(4a−1)(4a+3)))))])/da)=0 ((8(4a−13))/( (√(3(4a−1)^3 (4a+3)^3 ))))=0 a=((13)/4) min ((3/(sin γ))+(1/(tan α))) =4

$$\mathrm{wlog}\:{b}=\mathrm{1}\:\Rightarrow\:{c}={a}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\:\gamma\:={c}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\mathrm{cos}\:\alpha\:={a}^{\mathrm{2}} \\ $$$$\mathrm{cos}\:\gamma\:=\frac{\mathrm{3}−\mathrm{4}{a}}{\mathrm{8}{a}} \\ $$$$\mathrm{cos}\:\alpha\:=\frac{\mathrm{4}{a}+\mathrm{5}}{\mathrm{4}\left(\mathrm{2}{a}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{3}}{\mathrm{sin}\:\gamma}+\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}=\frac{\mathrm{28}{a}+\mathrm{5}}{\:\sqrt{\mathrm{3}\left(\mathrm{4}{a}−\mathrm{1}\right)\left(\mathrm{4}{a}+\mathrm{3}\right)}} \\ $$$$\frac{{d}\left[\frac{\mathrm{28}{a}+\mathrm{5}}{\:\sqrt{\mathrm{3}\left(\mathrm{4}{a}−\mathrm{1}\right)\left(\mathrm{4}{a}+\mathrm{3}\right)}}\right]}{{da}}=\mathrm{0} \\ $$$$\frac{\mathrm{8}\left(\mathrm{4}{a}−\mathrm{13}\right)}{\:\sqrt{\mathrm{3}\left(\mathrm{4}{a}−\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{4}{a}+\mathrm{3}\right)^{\mathrm{3}} }}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{13}}{\mathrm{4}} \\ $$$$\mathrm{min}\:\left(\frac{\mathrm{3}}{\mathrm{sin}\:\gamma}+\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}\right)\:=\mathrm{4} \\ $$

Answered by CrispyXYZ last updated on 11/Nov/24

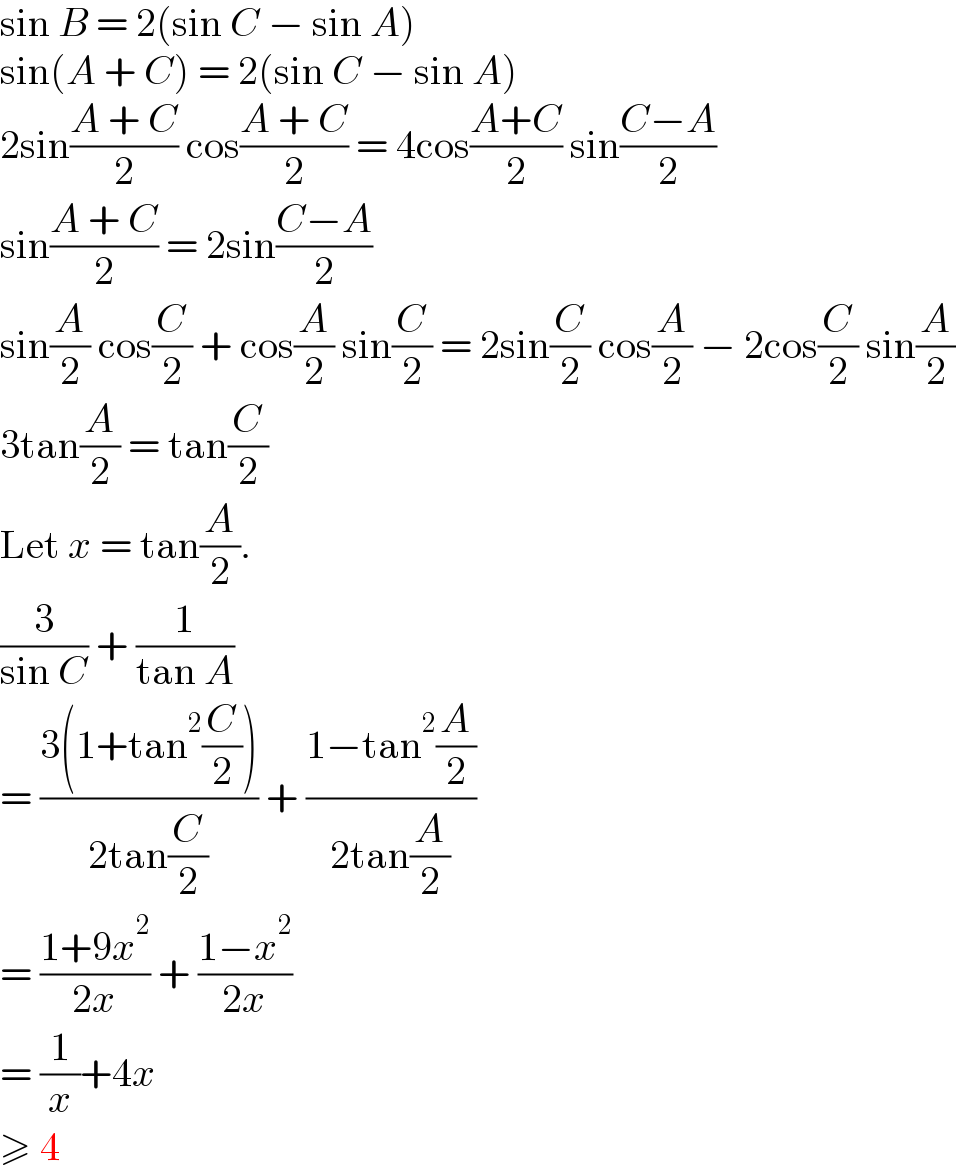
sin B = 2(sin C − sin A) sin(A + C) = 2(sin C − sin A) 2sin((A + C)/2) cos((A + C)/2) = 4cos((A+C)/2) sin((C−A)/2) sin((A + C)/2) = 2sin((C−A)/2) sin(A/2) cos(C/2) + cos(A/2) sin(C/2) = 2sin(C/2) cos(A/2) − 2cos(C/2) sin(A/2) 3tan(A/2) = tan(C/2) Let x = tan(A/2). (3/(sin C)) + (1/(tan A)) = ((3(1+tan^2 (C/2)))/(2tan(C/2))) + ((1−tan^2 (A/2))/(2tan(A/2))) = ((1+9x^2 )/(2x)) + ((1−x^2 )/(2x)) = (1/x)+4x ≥ 4

$$\mathrm{sin}\:{B}\:=\:\mathrm{2}\left(\mathrm{sin}\:{C}\:−\:\mathrm{sin}\:{A}\right) \\ $$$$\mathrm{sin}\left({A}\:+\:{C}\right)\:=\:\mathrm{2}\left(\mathrm{sin}\:{C}\:−\:\mathrm{sin}\:{A}\right) \\ $$$$\mathrm{2sin}\frac{{A}\:+\:{C}}{\mathrm{2}}\:\mathrm{cos}\frac{{A}\:+\:{C}}{\mathrm{2}}\:=\:\mathrm{4cos}\frac{{A}+{C}}{\mathrm{2}}\:\mathrm{sin}\frac{{C}−{A}}{\mathrm{2}} \\ $$$$\mathrm{sin}\frac{{A}\:+\:{C}}{\mathrm{2}}\:=\:\mathrm{2sin}\frac{{C}−{A}}{\mathrm{2}} \\ $$$$\mathrm{sin}\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\frac{{C}}{\mathrm{2}}\:+\:\mathrm{cos}\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\frac{{C}}{\mathrm{2}}\:=\:\mathrm{2sin}\frac{{C}}{\mathrm{2}}\:\mathrm{cos}\frac{{A}}{\mathrm{2}}\:−\:\mathrm{2cos}\frac{{C}}{\mathrm{2}}\:\mathrm{sin}\frac{{A}}{\mathrm{2}} \\ $$$$\mathrm{3tan}\frac{{A}}{\mathrm{2}}\:=\:\mathrm{tan}\frac{{C}}{\mathrm{2}} \\ $$$$\mathrm{Let}\:{x}\:=\:\mathrm{tan}\frac{{A}}{\mathrm{2}}. \\ $$$$\frac{\mathrm{3}}{\mathrm{sin}\:{C}}\:+\:\frac{\mathrm{1}}{\mathrm{tan}\:{A}} \\ $$$$=\:\frac{\mathrm{3}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \frac{{C}}{\mathrm{2}}\right)}{\mathrm{2tan}\frac{{C}}{\mathrm{2}}}\:+\:\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}}{\mathrm{2tan}\frac{{A}}{\mathrm{2}}} \\ $$$$=\:\frac{\mathrm{1}+\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}{x}}\:+\:\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{2}{x}} \\ $$$$=\:\frac{\mathrm{1}}{{x}}+\mathrm{4}{x} \\ $$$$\geqslant\:\mathrm{4} \\ $$

Commented by mnjuly1970 last updated on 10/Nov/24

((1/(x )) +4x)_(min) =4

$$\left(\frac{\mathrm{1}}{{x}\:}\:+\mathrm{4}{x}\right)_{{min}} =\mathrm{4} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com