Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 76579 by Rio Michael last updated on 28/Dec/19

A uniform ladder of weight W and length 2a rest in limiting equilibrium with one end on a rough horizontal ground and the other end on a rough vertical wall. The coefficient of friction between the ladder and the ground and between the ladder and the wall are respectively μ and λ . If the ladder makes an angle θ with the ground where tan θ = (5/(12)), a) show that 5μ + 6λμ − 6 = 0. b) find the value of λ and μ given that λμ =(1/2).

$$\mathrm{A}\:\mathrm{uniform}\:\mathrm{ladder}\:\mathrm{of}\:\mathrm{weight}\:{W}\:\mathrm{and}\:\mathrm{length} \\ $$$$\mathrm{2}{a}\:\mathrm{rest}\:\mathrm{in}\:\mathrm{limiting}\:\mathrm{equilibrium}\:\mathrm{with}\:\mathrm{one}\: \\ $$$$\mathrm{end}\:\mathrm{on}\:\mathrm{a}\:\mathrm{rough}\:\mathrm{horizontal}\:\mathrm{ground}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{other}\:\mathrm{end}\:\mathrm{on}\:\mathrm{a}\:\mathrm{rough}\:\mathrm{vertical}\:\mathrm{wall}. \\ $$$$\mathrm{The}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{friction}\:\mathrm{between}\:\mathrm{the}\:\mathrm{ladder} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{ground}\:\mathrm{and}\:\mathrm{between}\:\mathrm{the}\:\mathrm{ladder}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{wall}\:\mathrm{are}\:\mathrm{respectively}\:\mu\:\mathrm{and}\:\lambda\:.\:\mathrm{If}\:\mathrm{the}\:\mathrm{ladder} \\ $$$$\mathrm{makes}\:\mathrm{an}\:\mathrm{angle}\:\theta\:\mathrm{with}\:\mathrm{the}\:\mathrm{ground}\:\mathrm{where}\:\mathrm{tan}\:\theta\:=\:\frac{\mathrm{5}}{\mathrm{12}}, \\ $$$$\left.\mathrm{a}\right)\:\mathrm{show}\:\mathrm{that}\:\mathrm{5}\mu\:+\:\mathrm{6}\lambda\mu\:−\:\mathrm{6}\:=\:\mathrm{0}. \\ $$$$\left.\mathrm{b}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\lambda\:\mathrm{and}\:\mu\:\mathrm{given}\:\mathrm{that}\:\lambda\mu\:=\frac{\mathrm{1}}{\mathrm{2}}.\: \\ $$

Answered by mr W last updated on 28/Dec/19

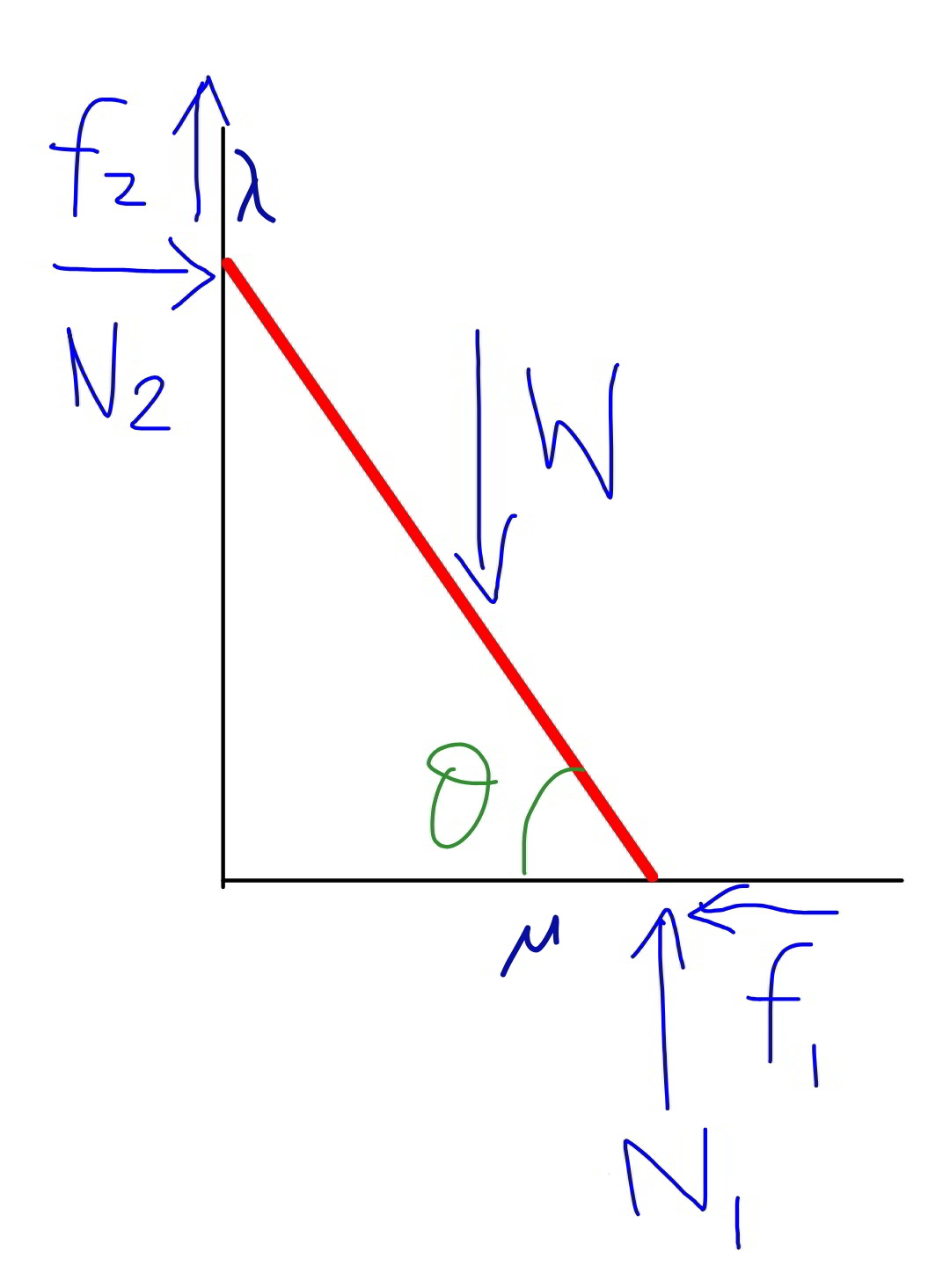
Commented by mr W last updated on 28/Dec/19

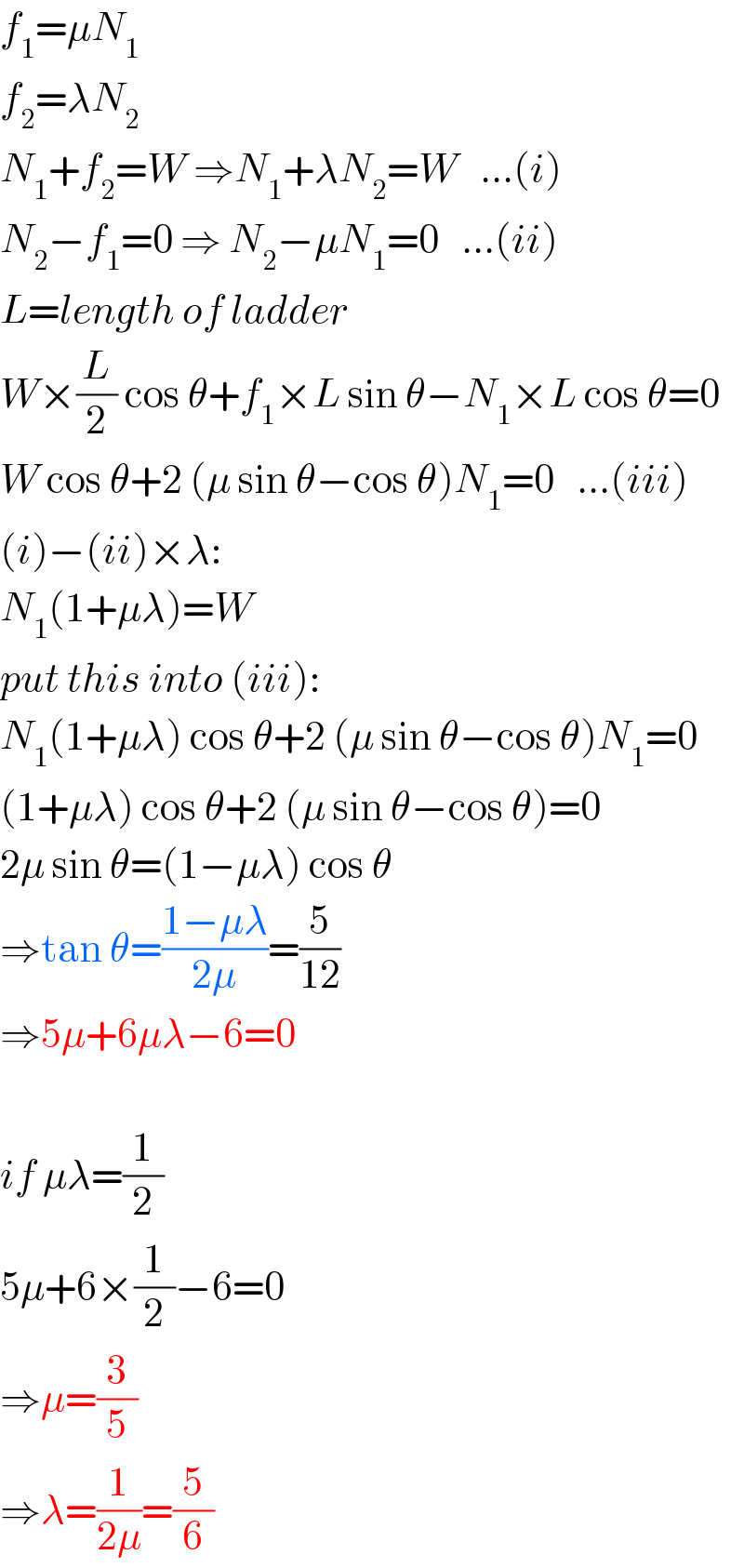
f_1 =μN_1 f_2 =λN_2 N_1 +f_2 =W ⇒N_1 +λN_2 =W ...(i) N_2 −f_1 =0 ⇒ N_2 −μN_1 =0 ...(ii) L=length of ladder W×(L/2) cos θ+f_1 ×L sin θ−N_1 ×L cos θ=0 W cos θ+2 (μ sin θ−cos θ)N_1 =0 ...(iii) (i)−(ii)×λ: N_1 (1+μλ)=W put this into (iii): N_1 (1+μλ) cos θ+2 (μ sin θ−cos θ)N_1 =0 (1+μλ) cos θ+2 (μ sin θ−cos θ)=0 2μ sin θ=(1−μλ) cos θ ⇒tan θ=((1−μλ)/(2μ))=(5/(12)) ⇒5μ+6μλ−6=0 if μλ=(1/2) 5μ+6×(1/2)−6=0 ⇒μ=(3/5) ⇒λ=(1/(2μ))=(5/6)

$${f}_{\mathrm{1}} =\mu{N}_{\mathrm{1}} \\ $$$${f}_{\mathrm{2}} =\lambda{N}_{\mathrm{2}} \\ $$$${N}_{\mathrm{1}} +{f}_{\mathrm{2}} ={W}\:\Rightarrow{N}_{\mathrm{1}} +\lambda{N}_{\mathrm{2}} ={W}\:\:\:...\left({i}\right) \\ $$$${N}_{\mathrm{2}} −{f}_{\mathrm{1}} =\mathrm{0}\:\Rightarrow\:{N}_{\mathrm{2}} −\mu{N}_{\mathrm{1}} =\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$${L}={length}\:{of}\:{ladder} \\ $$$${W}×\frac{{L}}{\mathrm{2}}\:\mathrm{cos}\:\theta+{f}_{\mathrm{1}} ×{L}\:\mathrm{sin}\:\theta−{N}_{\mathrm{1}} ×{L}\:\mathrm{cos}\:\theta=\mathrm{0} \\ $$$${W}\:\mathrm{cos}\:\theta+\mathrm{2}\:\left(\mu\:\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right){N}_{\mathrm{1}} =\mathrm{0}\:\:\:...\left({iii}\right) \\ $$$$\left({i}\right)−\left({ii}\right)×\lambda: \\ $$$${N}_{\mathrm{1}} \left(\mathrm{1}+\mu\lambda\right)={W} \\ $$$${put}\:{this}\:{into}\:\left({iii}\right): \\ $$$${N}_{\mathrm{1}} \left(\mathrm{1}+\mu\lambda\right)\:\mathrm{cos}\:\theta+\mathrm{2}\:\left(\mu\:\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right){N}_{\mathrm{1}} =\mathrm{0} \\ $$$$\left(\mathrm{1}+\mu\lambda\right)\:\mathrm{cos}\:\theta+\mathrm{2}\:\left(\mu\:\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)=\mathrm{0} \\ $$$$\mathrm{2}\mu\:\mathrm{sin}\:\theta=\left(\mathrm{1}−\mu\lambda\right)\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{1}−\mu\lambda}{\mathrm{2}\mu}=\frac{\mathrm{5}}{\mathrm{12}} \\ $$$$\Rightarrow\mathrm{5}\mu+\mathrm{6}\mu\lambda−\mathrm{6}=\mathrm{0} \\ $$$$ \\ $$$${if}\:\mu\lambda=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{5}\mu+\mathrm{6}×\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow\mu=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{2}\mu}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$

Commented by Rio Michael last updated on 28/Dec/19

thanks sir

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com