Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 217535 by ArshadS last updated on 15/Mar/25

A two-digit number is such that the sum of its digits is 10. When the digits are reversed, the new number is 28 less than twice the original number. Find the original number.

$$\mathrm{A}\:\mathrm{two}-\mathrm{digit}\:\mathrm{number}\:\mathrm{is}\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{its}\:\mathrm{digits}\:\mathrm{is}\:\mathrm{10}.\:\mathrm{When} \\ $$$$\mathrm{the}\:\mathrm{digits}\:\mathrm{are}\:\mathrm{reversed},\:\mathrm{the}\:\mathrm{new}\:\mathrm{number} \\ $$$$\:\mathrm{is}\:\mathrm{28}\:\mathrm{less}\:\mathrm{than}\:\mathrm{twice}\:\mathrm{the}\:\:\mathrm{original}\:\mathrm{number}. \\ $$$$\:\mathrm{Find}\:\mathrm{the}\:\mathrm{original}\:\mathrm{number}. \\ $$

Answered by aleks041103 last updated on 15/Mar/25

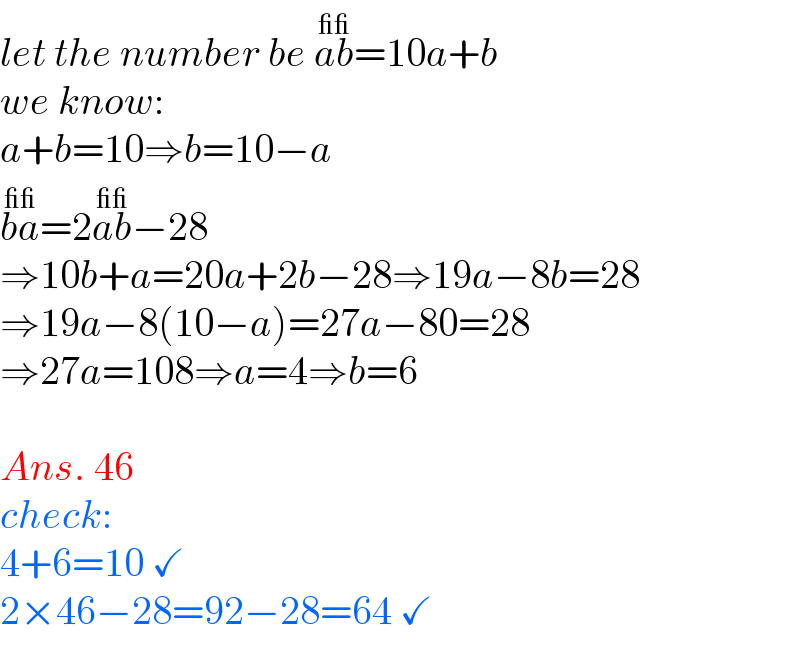
let the number be ab^(__) =10a+b we know: a+b=10⇒b=10−a ba^(__) =2ab^(__) −28 ⇒10b+a=20a+2b−28⇒19a−8b=28 ⇒19a−8(10−a)=27a−80=28 ⇒27a=108⇒a=4⇒b=6 Ans. 46 check: 4+6=10 ✓ 2×46−28=92−28=64 ✓

$${let}\:{the}\:{number}\:{be}\:\overset{\_\_} {{ab}}=\mathrm{10}{a}+{b} \\ $$$${we}\:{know}: \\ $$$${a}+{b}=\mathrm{10}\Rightarrow{b}=\mathrm{10}−{a} \\ $$$$\overset{\_\_} {{ba}}=\mathrm{2}\overset{\_\_} {{ab}}−\mathrm{28} \\ $$$$\Rightarrow\mathrm{10}{b}+{a}=\mathrm{20}{a}+\mathrm{2}{b}−\mathrm{28}\Rightarrow\mathrm{19}{a}−\mathrm{8}{b}=\mathrm{28} \\ $$$$\Rightarrow\mathrm{19}{a}−\mathrm{8}\left(\mathrm{10}−{a}\right)=\mathrm{27}{a}−\mathrm{80}=\mathrm{28} \\ $$$$\Rightarrow\mathrm{27}{a}=\mathrm{108}\Rightarrow{a}=\mathrm{4}\Rightarrow{b}=\mathrm{6} \\ $$$$ \\ $$$${Ans}.\:\mathrm{46} \\ $$$${check}: \\ $$$$\mathrm{4}+\mathrm{6}=\mathrm{10}\:\checkmark \\ $$$$\mathrm{2}×\mathrm{46}−\mathrm{28}=\mathrm{92}−\mathrm{28}=\mathrm{64}\:\checkmark \\ $$

Commented by ArshadS last updated on 16/Mar/25

Thanks sir!

$$\boldsymbol{\mathrm{T}}\mathrm{hanks}\:\boldsymbol{\mathrm{s}}\mathrm{ir}! \\ $$

Answered by Rasheed.Sindhi last updated on 16/Mar/25

Let a & 10−a are digits •Original number=10a+(10−a) =9a+10 •Reversed number=10(10−a)+a =100−9a •100−9a=2(9a+10)−28 100−9a=18a+20−28 27a=108⇒a=4 Original number=9(4)+10=46 Verification: Reversed number=100−9(4)=64

$${Let}\:{a}\:\&\:\mathrm{10}−{a}\:{are}\:{digits} \\ $$$$\bullet{Original}\:{number}=\mathrm{10}{a}+\left(\mathrm{10}−{a}\right) \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{9}{a}+\mathrm{10} \\ $$$$\bullet{Reversed}\:{number}=\mathrm{10}\left(\mathrm{10}−{a}\right)+{a} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{100}−\mathrm{9}{a} \\ $$$$\bullet\mathrm{100}−\mathrm{9}{a}=\mathrm{2}\left(\mathrm{9}{a}+\mathrm{10}\right)−\mathrm{28} \\ $$$$\:\:\:\mathrm{100}−\mathrm{9}{a}=\mathrm{18}{a}+\mathrm{20}−\mathrm{28} \\ $$$$\:\:\:\:\:\mathrm{27}{a}=\mathrm{108}\Rightarrow{a}=\mathrm{4} \\ $$$${Original}\:{number}=\mathrm{9}\left(\mathrm{4}\right)+\mathrm{10}=\mathrm{46} \\ $$$$\mathcal{V}{erification}: \\ $$$${Reversed}\:{number}=\mathrm{100}−\mathrm{9}\left(\mathrm{4}\right)=\mathrm{64} \\ $$

Commented by ArshadS last updated on 19/Mar/25

Thanks sir!

$$\mathrm{Thanks}\:\mathrm{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com