
Question Number 178561 by Huy last updated on 18/Oct/22
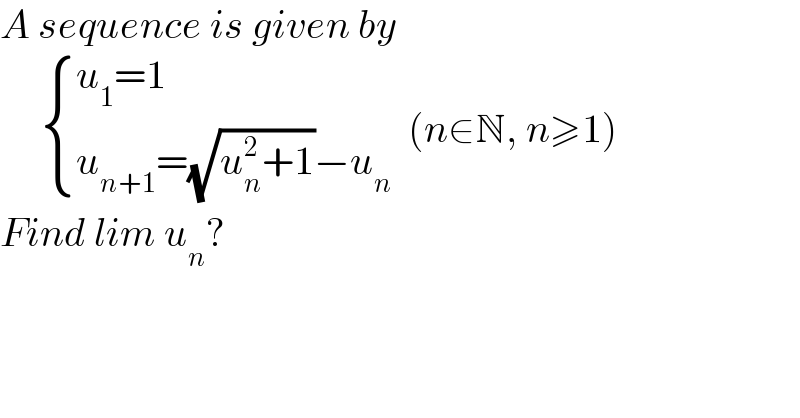
$${A}\:{sequence}\:{is}\:{given}\:{by}\: \\ $$$$\:\:\:\:\:\begin{cases}{{u}_{\mathrm{1}} =\mathrm{1}}\\{{u}_{{n}+\mathrm{1}} =\sqrt{{u}_{{n}} ^{\mathrm{2}} +\mathrm{1}}−{u}_{{n}} }\end{cases}\:\:\left({n}\in\mathbb{N},\:{n}\geqslant\mathrm{1}\right) \\ $$$${Find}\:{lim}\:{u}_{{n}} ? \\ $$
Answered by mr W last updated on 18/Oct/22
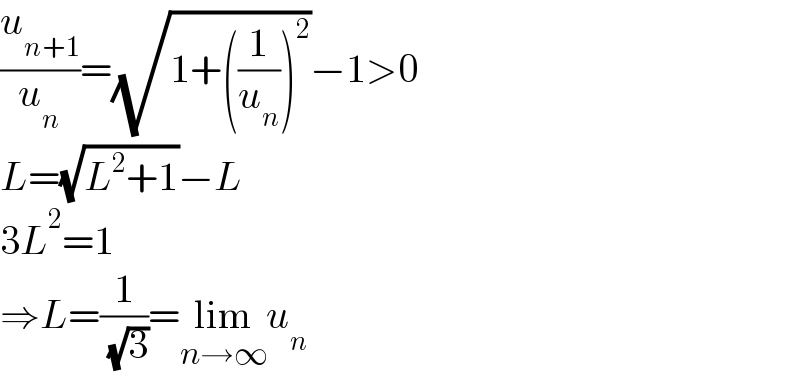
$$\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }=\sqrt{\mathrm{1}+\left(\frac{\mathrm{1}}{{u}_{{n}} }\right)^{\mathrm{2}} }−\mathrm{1}>\mathrm{0} \\ $$$${L}=\sqrt{{L}^{\mathrm{2}} +\mathrm{1}}−{L} \\ $$$$\mathrm{3}{L}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{L}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{u}_{{n}} \\ $$
