
Question Number 217425 by Jubr last updated on 13/Mar/25

A restaurant offers 5 choices of appetizer, 10 choices of main meal and 4 choices of dessert. A customer can choose to eat just one course, or two different courses, or all three courses. Assuming all choices are available, how many different possible meals does the restaurant offer?
Answered by mr W last updated on 13/Mar/25
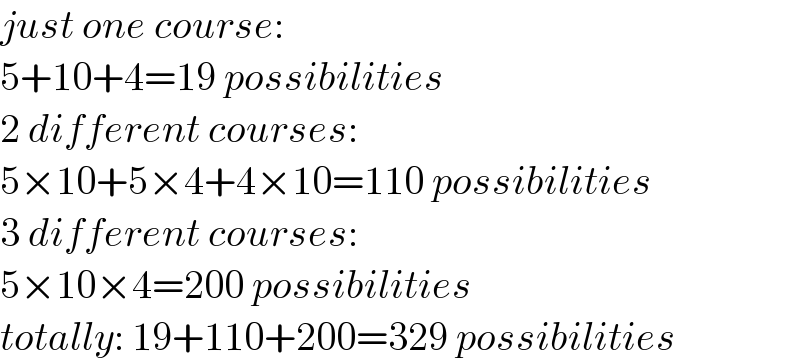
$${just}\:{one}\:{course}: \\ $$$$\mathrm{5}+\mathrm{10}+\mathrm{4}=\mathrm{19}\:{possibilities} \\ $$$$\mathrm{2}\:{different}\:{courses}: \\ $$$$\mathrm{5}×\mathrm{10}+\mathrm{5}×\mathrm{4}+\mathrm{4}×\mathrm{10}=\mathrm{110}\:{possibilities} \\ $$$$\mathrm{3}\:{different}\:{courses}: \\ $$$$\mathrm{5}×\mathrm{10}×\mathrm{4}=\mathrm{200}\:{possibilities} \\ $$$${totally}:\:\mathrm{19}+\mathrm{110}+\mathrm{200}=\mathrm{329}\:{possibilities} \\ $$
Commented by Jubr last updated on 14/Mar/25

$${Thanks}\:{sir}. \\ $$$${I}\:{appreciate}. \\ $$
Answered by MathematicalUser2357 last updated on 14/Mar/25

$$\: \cancel{\underbrace{ }} \\ $$
Commented by mr W last updated on 14/Mar/25

$${how}\:{did}\:{you}\:{get}? \\ $$
