
Question Number 84651 by ajfour last updated on 14/Mar/20

$${A}\:{person}\:{stands}\:{in}\:{the}\:{diagonal} \\ $$$${produced}\:{of}\:{the}\:{square}\:{base}\:{of}\:{a} \\ $$$${church}\:{tower},\:{at}\:{a}\:{distance}\:\mathrm{2}{a} \\ $$$${from}\:{it},\:{and}\:{observes}\:{the}\:{angle} \\ $$$${of}\:{elevation}\:{of}\:{each}\:{of}\:{the}\:{two} \\ $$$${outer}\:{corners}\:{of}\:{the}\:{top}\:{of}\:{the} \\ $$$${tower}\:{to}\:{be}\:\mathrm{30}°,\:{while}\:{that}\:{of}\:{the} \\ $$$${nearest}\:{corner}\:{is}\:\mathrm{45}°.\:{Find}\:{the} \\ $$$${breadth}\:{of}\:{the}\:{tower}. \\ $$
Answered by mr W last updated on 14/Mar/20
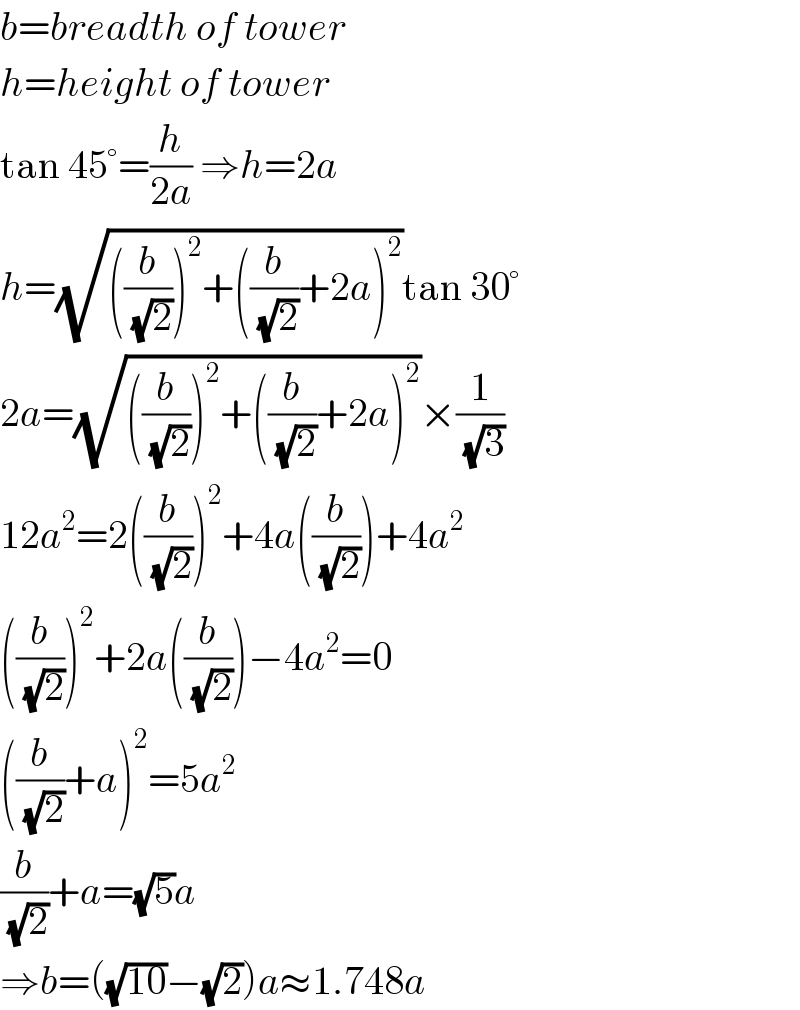
$${b}={breadth}\:{of}\:{tower} \\ $$$${h}={height}\:{of}\:{tower} \\ $$$$\mathrm{tan}\:\mathrm{45}°=\frac{{h}}{\mathrm{2}{a}}\:\Rightarrow{h}=\mathrm{2}{a} \\ $$$${h}=\sqrt{\left(\frac{{b}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\left(\frac{{b}}{\sqrt{\mathrm{2}}}+\mathrm{2}{a}\right)^{\mathrm{2}} }\mathrm{tan}\:\mathrm{30}° \\ $$$$\mathrm{2}{a}=\sqrt{\left(\frac{{b}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\left(\frac{{b}}{\sqrt{\mathrm{2}}}+\mathrm{2}{a}\right)^{\mathrm{2}} }×\frac{\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$$$\mathrm{12}{a}^{\mathrm{2}} =\mathrm{2}\left(\frac{{b}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{4}{a}\left(\frac{{b}}{\sqrt{\mathrm{2}}}\right)+\mathrm{4}{a}^{\mathrm{2}} \\ $$$$\left(\frac{{b}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{2}{a}\left(\frac{{b}}{\sqrt{\mathrm{2}}}\right)−\mathrm{4}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\frac{{b}}{\sqrt{\mathrm{2}}}+{a}\right)^{\mathrm{2}} =\mathrm{5}{a}^{\mathrm{2}} \\ $$$$\frac{{b}}{\sqrt{\mathrm{2}}}+{a}=\sqrt{\mathrm{5}}{a} \\ $$$$\Rightarrow{b}=\left(\sqrt{\mathrm{10}}−\sqrt{\mathrm{2}}\right){a}\approx\mathrm{1}.\mathrm{748}{a} \\ $$
Commented by ajfour last updated on 14/Mar/20
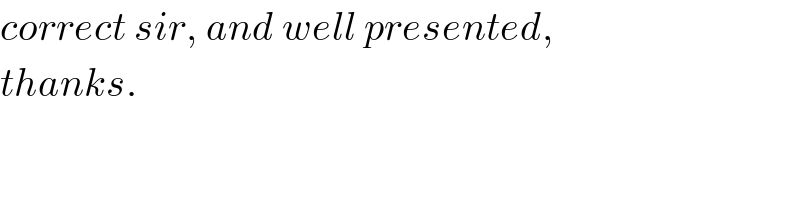
$${correct}\:{sir},\:{and}\:{well}\:{presented}, \\ $$$${thanks}. \\ $$
