
Question Number 166929 by MathsFan last updated on 02/Mar/22

$$\:{A}\:{particle}\:{of}\:{mass}\:\mathrm{0}.\mathrm{25}{kg}\:{vibrates} \\ $$$$\:{with}\:{a}\:{period}\:{of}\:\mathrm{2}{secs}.\:{If}\:{its}\: \\ $$$$\:{greatest}\:{displacement}\:{is}\:\mathrm{0}.\mathrm{4}{m}.\:{What} \\ $$$$\:{is}\:{its}\:{maximum}\:{kinetic}\:{energy}. \\ $$
Answered by mr W last updated on 02/Mar/22
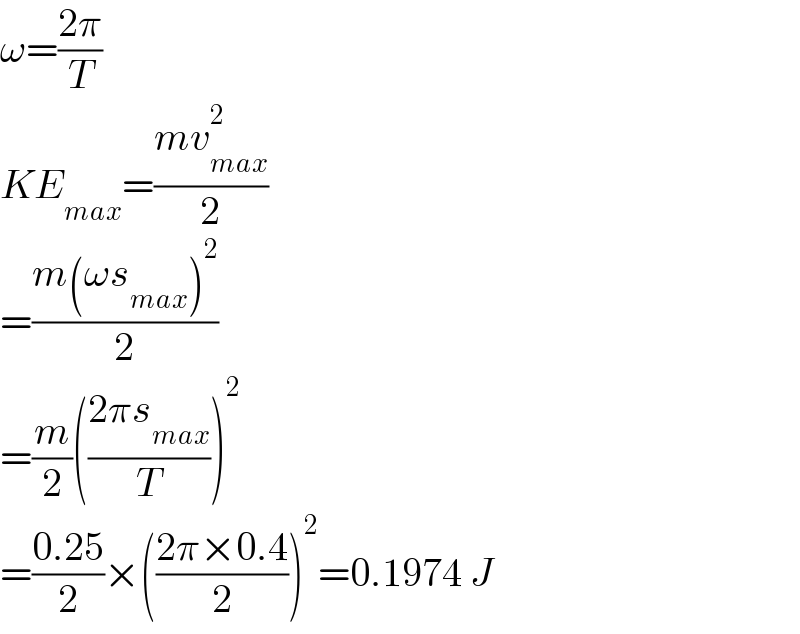
$$\omega=\frac{\mathrm{2}\pi}{{T}} \\ $$$${KE}_{{max}} =\frac{{mv}_{{max}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\frac{{m}\left(\omega{s}_{{max}} \right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\frac{{m}}{\mathrm{2}}\left(\frac{\mathrm{2}\pi{s}_{{max}} }{{T}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{0}.\mathrm{25}}{\mathrm{2}}×\left(\frac{\mathrm{2}\pi×\mathrm{0}.\mathrm{4}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{0}.\mathrm{1974}\:{J} \\ $$
Commented by MathsFan last updated on 02/Mar/22
$${thank}\:{you}\:{champion} \\ $$
