
Question Number 198496 by mnjuly1970 last updated on 21/Oct/23
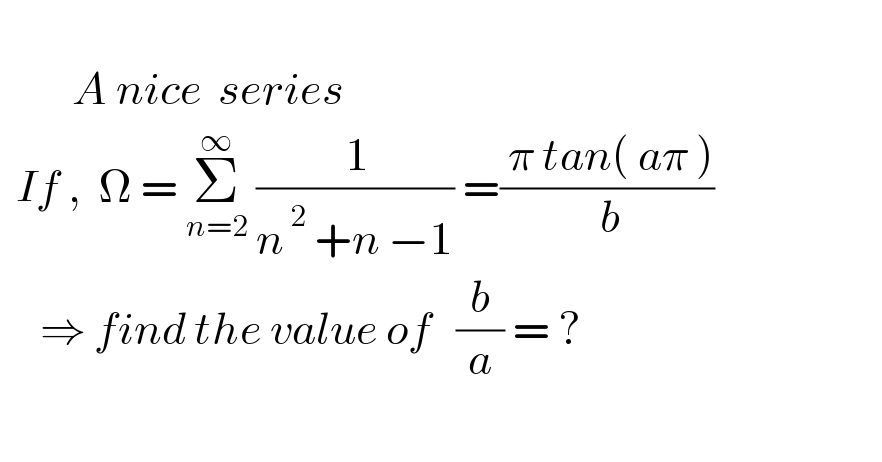
$$ \\ $$$$\:\:\:\:\:\:\:\:\:{A}\:{nice}\:\:{series} \\ $$$$\:\:{If}\:,\:\:\Omega\:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{\:\mathrm{1}}{{n}^{\:\mathrm{2}} \:+{n}\:−\mathrm{1}}\:=\frac{\:\pi\:{tan}\left(\:{a}\pi\:\right)}{\:{b}} \\ $$$$\:\:\:\:\:\Rightarrow\:{find}\:{the}\:{value}\:{of}\:\:\:\frac{{b}}{{a}}\:=\:? \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
Answered by mr W last updated on 21/Oct/23
![Ω=Σ_(n=2) ^∞ (1/(n^2 +n−1))=Σ_(n=1) ^∞ (1/(n^2 +n−1))−1 Σ_(n=1) ^∞ (1/(n^2 +n−1)) =Σ_(n=1) ^∞ (1/((n−p)(n−q))) with p, q=((−1±(√5))/2) and p+q=−1, pq=−1 =(1/(p−q))Σ_(n=1) ^∞ ((1/(n−p))−(1/(n−q))) =(1/(p−q))[ψ(1−q)−ψ(1−p)] =(1/(p−q))[ψ(1+1+p)−ψ(1−p)] =(1/(p−q))[ψ(1+p)+(1/(1+p))−ψ(1−p)] =(1/(q−p))[ψ(p)+(1/p)+(1/(1+p))−ψ(p)−π cot pπ] =(1/(p−q))[(1/p)+(1/(1+p))−π cot pπ] =(1/(p−q))[(1/p)−(1/q)−π cot pπ] =(1/(p−q))[((q−p)/(pq))−π cot pπ] =−(1/(pq))−(π/(p−q)) cot pπ =1−(π/( (√5))) cot (((−1+(√5))π)/2) =1+(π/( (√5))) cot ((π/2)−(((√5)π)/2)) =1+(π/( (√5))) tan (((√5)π)/2) Ω=1+(π/( (√5))) tan (((√5)π)/2)−1 Ω=(π/( (√5))) tan (((√5)π)/2)=((πtan (aπ))/b) ⇒a=((√5)/2), b=(√5) ⇒(b/a)=2](Q198506.png)
$$\Omega=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}−\mathrm{1}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}−\mathrm{1}}−\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}−\mathrm{1}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−{p}\right)\left({n}−{q}\right)}\:\:{with}\:{p},\:{q}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\:{and}\:{p}+{q}=−\mathrm{1},\:{pq}=−\mathrm{1} \\ $$$$=\frac{\mathrm{1}}{{p}−{q}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}−{p}}−\frac{\mathrm{1}}{{n}−{q}}\right) \\ $$$$=\frac{\mathrm{1}}{{p}−{q}}\left[\psi\left(\mathrm{1}−{q}\right)−\psi\left(\mathrm{1}−{p}\right)\right] \\ $$$$=\frac{\mathrm{1}}{{p}−{q}}\left[\psi\left(\mathrm{1}+\mathrm{1}+{p}\right)−\psi\left(\mathrm{1}−{p}\right)\right] \\ $$$$=\frac{\mathrm{1}}{{p}−{q}}\left[\psi\left(\mathrm{1}+{p}\right)+\frac{\mathrm{1}}{\mathrm{1}+{p}}−\psi\left(\mathrm{1}−{p}\right)\right] \\ $$$$=\frac{\mathrm{1}}{{q}−{p}}\left[\psi\left({p}\right)+\frac{\mathrm{1}}{{p}}+\frac{\mathrm{1}}{\mathrm{1}+{p}}−\psi\left({p}\right)−\pi\:\mathrm{cot}\:{p}\pi\right] \\ $$$$=\frac{\mathrm{1}}{{p}−{q}}\left[\frac{\mathrm{1}}{{p}}+\frac{\mathrm{1}}{\mathrm{1}+{p}}−\pi\:\mathrm{cot}\:{p}\pi\right] \\ $$$$=\frac{\mathrm{1}}{{p}−{q}}\left[\frac{\mathrm{1}}{{p}}−\frac{\mathrm{1}}{{q}}−\pi\:\mathrm{cot}\:{p}\pi\right] \\ $$$$=\frac{\mathrm{1}}{{p}−{q}}\left[\frac{{q}−{p}}{{pq}}−\pi\:\mathrm{cot}\:{p}\pi\right] \\ $$$$=−\frac{\mathrm{1}}{{pq}}−\frac{\pi}{{p}−{q}}\:\mathrm{cot}\:{p}\pi \\ $$$$=\mathrm{1}−\frac{\pi}{\:\sqrt{\mathrm{5}}}\:\mathrm{cot}\:\frac{\left(−\mathrm{1}+\sqrt{\mathrm{5}}\right)\pi}{\mathrm{2}} \\ $$$$=\mathrm{1}+\frac{\pi}{\:\sqrt{\mathrm{5}}}\:\mathrm{cot}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}\pi}{\mathrm{2}}\right) \\ $$$$=\mathrm{1}+\frac{\pi}{\:\sqrt{\mathrm{5}}}\:\mathrm{tan}\:\frac{\sqrt{\mathrm{5}}\pi}{\mathrm{2}} \\ $$$$\Omega=\mathrm{1}+\frac{\pi}{\:\sqrt{\mathrm{5}}}\:\mathrm{tan}\:\frac{\sqrt{\mathrm{5}}\pi}{\mathrm{2}}−\mathrm{1} \\ $$$$\Omega=\frac{\pi}{\:\sqrt{\mathrm{5}}}\:\mathrm{tan}\:\frac{\sqrt{\mathrm{5}}\pi}{\mathrm{2}}=\frac{\pi\mathrm{tan}\:\left({a}\pi\right)}{{b}} \\ $$$$\Rightarrow{a}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}},\:{b}=\sqrt{\mathrm{5}}\:\Rightarrow\frac{{b}}{{a}}=\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 21/Oct/23
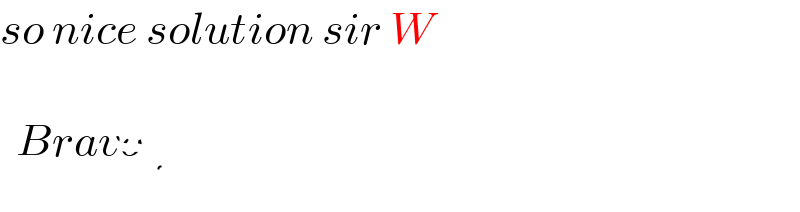
$${so}\:{nice}\:{solution}\:{sir}\:{W} \\ $$$$\:\:{Bravo}\:\:\underline{\underbrace{ }} \\ $$
