
Question Number 131343 by physicstutes last updated on 03/Feb/21

$$\mathrm{A}\:\mathrm{mapping}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{as}\:{G}\rightarrow{S}\:\mathrm{where}\:\left({G},×\right)\:\mathrm{and}\:\left({S},+\right), \\ $$$$\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{mapping}\:{f}\left({x}\right)\:=\:\mathrm{ln}\:{x}\:\mathrm{is}\:\mathrm{an}\:\mathrm{isomophism}. \\ $$
Answered by mindispower last updated on 04/Feb/21
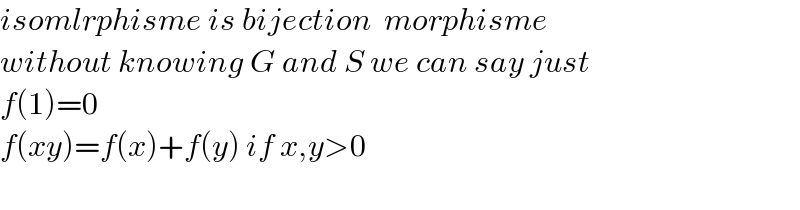
$${isomlrphisme}\:{is}\:{bijection}\:\:{morphisme} \\ $$$${without}\:{knowing}\:{G}\:{and}\:{S}\:{we}\:{can}\:{say}\:{just} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${f}\left({xy}\right)={f}\left({x}\right)+{f}\left({y}\right)\:{if}\:{x},{y}>\mathrm{0} \\ $$$$ \\ $$
