
Question Number 196774 by BaliramKumar last updated on 31/Aug/23

$$ \\ $$A man standing on top of Burj Khalifa. If the height of Burj Khalifa including a man is 830 m, then what is the maximum distance up to which a man can see objects on Earth? (Earth's radius 6371 km)
Answered by Frix last updated on 31/Aug/23

$${h}=.\mathrm{83km} \\ $$$${r}=\mathrm{6371km} \\ $$$$ \\ $$$$\left({h}+{r}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +{r}^{\mathrm{2}} \\ $$$${x}=\sqrt{{h}\left({h}+\mathrm{2}{r}\right)}\approx\mathrm{102}.\mathrm{84km} \\ $$
Commented by BaliramKumar last updated on 31/Aug/23
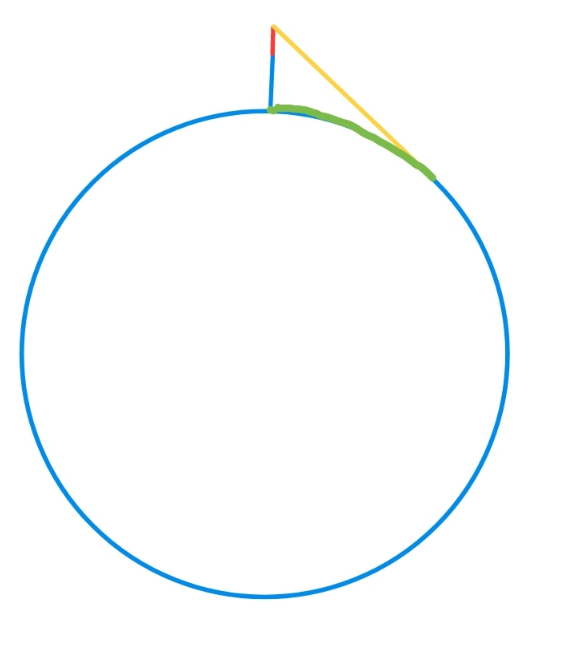
Commented by BaliramKumar last updated on 31/Aug/23
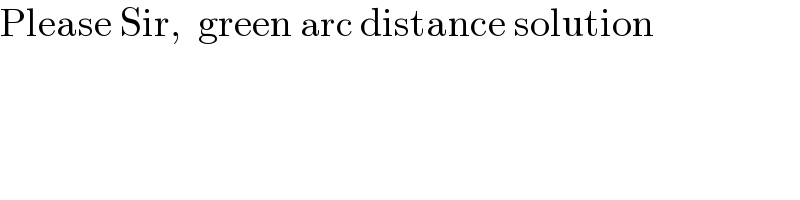
$$\mathrm{Please}\:\mathrm{Sir},\:\:\mathrm{green}\:\mathrm{arc}\:\mathrm{distance}\:\mathrm{solution} \\ $$
Commented by mahdipoor last updated on 31/Aug/23

$${cos}\alpha=\frac{{r}}{{h}+{r}}\:,\:{arc}={r}\alpha \\ $$
Commented by Frix last updated on 01/Sep/23

$$\mathrm{Yes}. \\ $$
Commented by mr W last updated on 01/Sep/23

$$\alpha=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{6371}}{\mathrm{6371}+\mathrm{0}.\mathrm{83}}\approx\mathrm{0} \\ $$$$\alpha\approx\mathrm{tan}\:\alpha \\ $$$${arc}={r}\alpha\approx{r}\:\mathrm{tan}\:\alpha={x} \\ $$$${compare}: \\ $$$${arc}={ra}=\mathrm{102}.\mathrm{833}\:{km} \\ $$$${x}={r}\:\mathrm{tan}\:\alpha=\mathrm{102}.\mathrm{842}\:{km} \\ $$
Commented by BaliramKumar last updated on 01/Sep/23

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
