
Question Number 22892 by NECx last updated on 23/Oct/17

$${A}\:{horizontal}\:{force}\:{of}\:\mathrm{10}{N}\:{just} \\ $$$${prevents}\:{a}\:{mass}\:{of}\:\mathrm{2}{kg}\:{from} \\ $$$${sliding}\:{down}\:{a}\:{rough}\:{plane} \\ $$$${inclined}\:{at}\:\mathrm{45}°\:{to}\:{the}\:{horizontal}. \\ $$$${Find}\:{the}\:{coefficient}\:{of}\:{friction}. \\ $$
Commented by ajfour last updated on 23/Oct/17
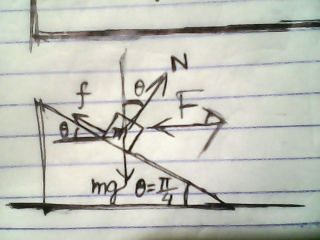
Commented by ajfour last updated on 23/Oct/17
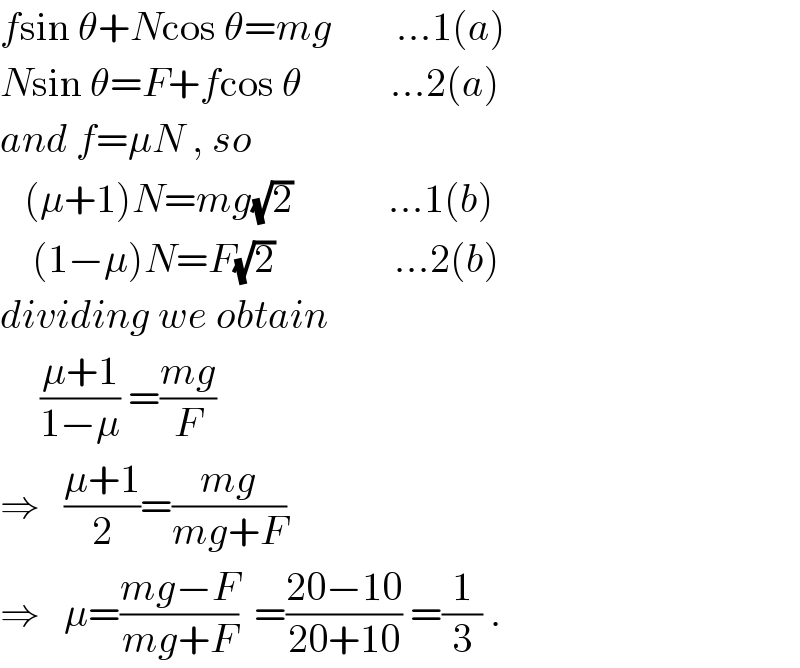
$${f}\mathrm{sin}\:\theta+{N}\mathrm{cos}\:\theta={mg}\:\:\:\:\:\:\:\:...\mathrm{1}\left({a}\right) \\ $$$${N}\mathrm{sin}\:\theta={F}+{f}\mathrm{cos}\:\theta\:\:\:\:\:\:\:\:\:\:\:...\mathrm{2}\left({a}\right) \\ $$$${and}\:{f}=\mu{N}\:,\:{so} \\ $$$$\:\:\:\left(\mu+\mathrm{1}\right){N}={mg}\sqrt{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:...\mathrm{1}\left({b}\right) \\ $$$$\:\:\:\:\left(\mathrm{1}−\mu\right){N}={F}\sqrt{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\mathrm{2}\left({b}\right) \\ $$$${dividing}\:{we}\:{obtain} \\ $$$$\:\:\:\:\:\frac{\mu+\mathrm{1}}{\mathrm{1}−\mu}\:=\frac{{mg}}{{F}} \\ $$$$\Rightarrow\:\:\:\frac{\mu+\mathrm{1}}{\mathrm{2}}=\frac{{mg}}{{mg}+{F}} \\ $$$$\Rightarrow\:\:\:\mu=\frac{{mg}−{F}}{{mg}+{F}}\:\:=\frac{\mathrm{20}−\mathrm{10}}{\mathrm{20}+\mathrm{10}}\:=\frac{\mathrm{1}}{\mathrm{3}}\:. \\ $$
Commented by NECx last updated on 24/Oct/17
$${your}\:{answer}\:{is}\:{very}\:{accurate}\:{sir}. \\ $$$${Thanks}\:{for}\:{the}\:{help} \\ $$
