
Question Number 19472 by Tinkutara last updated on 11/Aug/17

$$\mathrm{A}\:\mathrm{fishing}\:\mathrm{boat}\:\mathrm{is}\:\mathrm{anchored}\:\mathrm{9}\:\mathrm{km}\:\mathrm{away} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{nearest}\:\mathrm{point}\:\mathrm{on}\:\mathrm{the}\:\mathrm{shore}.\:\mathrm{A} \\ $$$$\mathrm{messanger}\:\mathrm{must}\:\mathrm{be}\:\mathrm{sent}\:\mathrm{from}\:\mathrm{the}\:\mathrm{fishing} \\ $$$$\mathrm{boat}\:\mathrm{to}\:\mathrm{a}\:\mathrm{camp},\:\mathrm{15}\:\mathrm{km}\:\mathrm{from}\:\mathrm{the}\:\mathrm{point} \\ $$$$\mathrm{on}\:\mathrm{shore}\:\mathrm{closest}\:\mathrm{to}\:\mathrm{boat}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{messanger} \\ $$$$\mathrm{can}\:\mathrm{walk}\:\mathrm{at}\:\mathrm{a}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{5}\:\mathrm{km}\:\mathrm{per}\:\mathrm{hour} \\ $$$$\mathrm{and}\:\mathrm{can}\:\mathrm{row}\:\mathrm{at}\:\mathrm{4}\:\mathrm{km}/\mathrm{h},\:\mathrm{determine}\:\mathrm{the} \\ $$$$\mathrm{distance}\:\mathrm{of}\:\mathrm{that}\:\mathrm{point}\:\left(\mathrm{in}\:\mathrm{km}\right)\:\mathrm{from}\:\mathrm{the} \\ $$$$\mathrm{shore},\:\mathrm{where}\:\mathrm{he}\:\mathrm{must}\:\mathrm{land}\:\mathrm{so}\:\mathrm{as}\:\mathrm{to} \\ $$$$\mathrm{reach}\:\mathrm{the}\:\mathrm{shore}\:\mathrm{in}\:\mathrm{least}\:\mathrm{possible}\:\mathrm{time}. \\ $$
Commented by Tinkutara last updated on 11/Aug/17
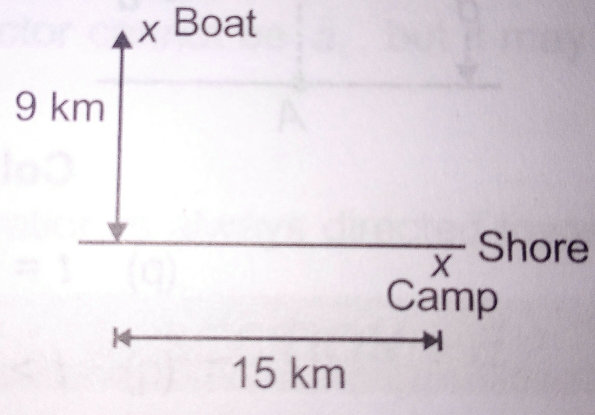
Commented by mrW1 last updated on 11/Aug/17
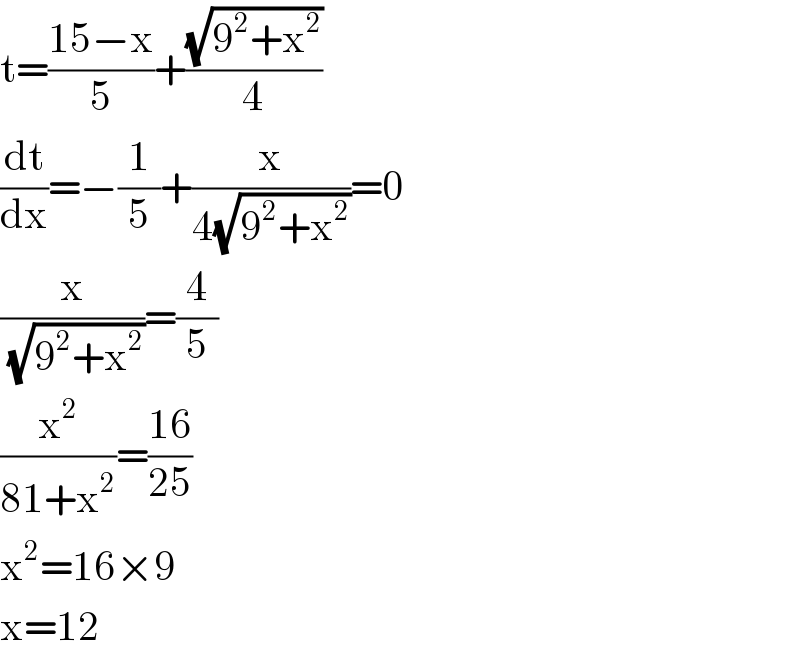
$$\mathrm{t}=\frac{\mathrm{15}−\mathrm{x}}{\mathrm{5}}+\frac{\sqrt{\mathrm{9}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }}{\mathrm{4}} \\ $$$$\frac{\mathrm{dt}}{\mathrm{dx}}=−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{x}}{\mathrm{4}\sqrt{\mathrm{9}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\frac{\mathrm{x}}{\sqrt{\mathrm{9}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{81}+\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{16}}{\mathrm{25}} \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{16}×\mathrm{9} \\ $$$$\mathrm{x}=\mathrm{12} \\ $$
Commented by Tinkutara last updated on 12/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
