Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 5291 by Rasheed Soomro last updated on 05/May/16

A circle has been drawn with one unit opened compass on surface of a sphere of one unit radius. What will be the area of the circle?

$$\mathrm{A}\:\mathrm{circle}\:\mathrm{has}\:\mathrm{been}\:\mathrm{drawn}\:\mathrm{with}\:\mathrm{one} \\ $$$$\mathrm{unit}\:\mathrm{opened}\:\mathrm{compass}\:\mathrm{on}\:\:\mathrm{surface} \\ $$$$\mathrm{of}\:\mathrm{a}\:\mathrm{sphere}\:\mathrm{of}\:\mathrm{one}\:\mathrm{unit}\:\mathrm{radius}.\: \\ $$$$\mathrm{What}\:\mathrm{will}\:\mathrm{be}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}? \\ $$

Commented by Yozzii last updated on 05/May/16

A=0.75π

$${A}=\mathrm{0}.\mathrm{75}\pi \\ $$

Commented by Yozzii last updated on 05/May/16

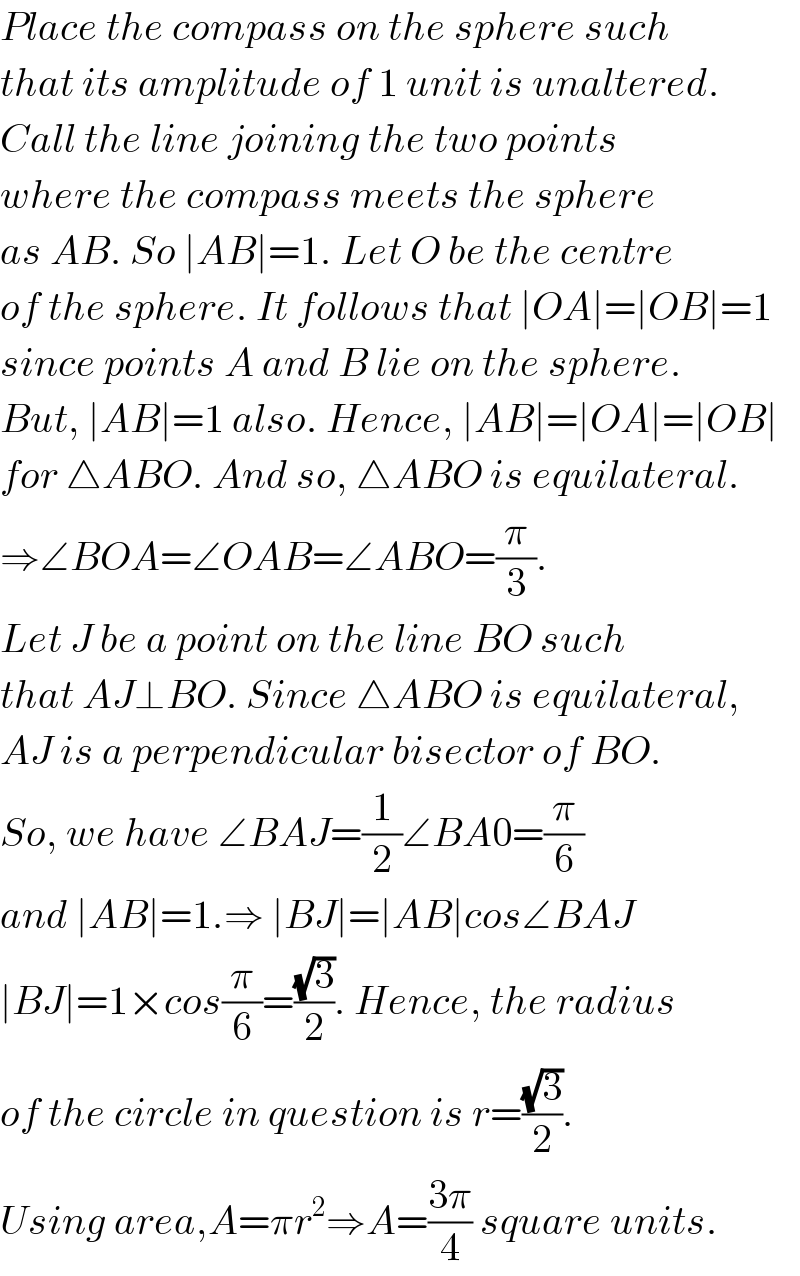
Place the compass on the sphere such that its amplitude of 1 unit is unaltered. Call the line joining the two points where the compass meets the sphere as AB. So ∣AB∣=1. Let O be the centre of the sphere. It follows that ∣OA∣=∣OB∣=1 since points A and B lie on the sphere. But, ∣AB∣=1 also. Hence, ∣AB∣=∣OA∣=∣OB∣ for △ABO. And so, △ABO is equilateral. ⇒∠BOA=∠OAB=∠ABO=(π/3). Let J be a point on the line BO such that AJ⊥BO. Since △ABO is equilateral, AJ is a perpendicular bisector of BO. So, we have ∠BAJ=(1/2)∠BA0=(π/6) and ∣AB∣=1.⇒ ∣BJ∣=∣AB∣cos∠BAJ ∣BJ∣=1×cos(π/6)=((√3)/2). Hence, the radius of the circle in question is r=((√3)/2). Using area,A=πr^2 ⇒A=((3π)/4) square units.

$${Place}\:{the}\:{compass}\:{on}\:{the}\:{sphere}\:{such} \\ $$$${that}\:{its}\:{amplitude}\:{of}\:\mathrm{1}\:{unit}\:{is}\:{unaltered}. \\ $$$${Call}\:{the}\:{line}\:{joining}\:{the}\:{two}\:{points} \\ $$$${where}\:{the}\:{compass}\:{meets}\:{the}\:{sphere}\: \\ $$$${as}\:{AB}.\:{So}\:\mid{AB}\mid=\mathrm{1}.\:{Let}\:{O}\:{be}\:{the}\:{centre} \\ $$$${of}\:{the}\:{sphere}.\:{It}\:{follows}\:{that}\:\mid{OA}\mid=\mid{OB}\mid=\mathrm{1} \\ $$$${since}\:{points}\:{A}\:{and}\:{B}\:{lie}\:{on}\:{the}\:{sphere}. \\ $$$${But},\:\mid{AB}\mid=\mathrm{1}\:{also}.\:{Hence},\:\mid{AB}\mid=\mid{OA}\mid=\mid{OB}\mid \\ $$$${for}\:\bigtriangleup{ABO}.\:{And}\:{so},\:\bigtriangleup{ABO}\:{is}\:{equilateral}. \\ $$$$\Rightarrow\angle{BOA}=\angle{OAB}=\angle{ABO}=\frac{\pi}{\mathrm{3}}.\: \\ $$$${Let}\:{J}\:{be}\:{a}\:{point}\:{on}\:{the}\:{line}\:{BO}\:{such} \\ $$$${that}\:{AJ}\bot{BO}.\:{Since}\:\bigtriangleup{ABO}\:{is}\:{equilateral}, \\ $$$${AJ}\:{is}\:{a}\:{perpendicular}\:{bisector}\:{of}\:{BO}. \\ $$$${So},\:{we}\:{have}\:\angle{BAJ}=\frac{\mathrm{1}}{\mathrm{2}}\angle{BA}\mathrm{0}=\frac{\pi}{\mathrm{6}} \\ $$$${and}\:\mid{AB}\mid=\mathrm{1}.\Rightarrow\:\mid{BJ}\mid=\mid{AB}\mid{cos}\angle{BAJ} \\ $$$$\mid{BJ}\mid=\mathrm{1}×{cos}\frac{\pi}{\mathrm{6}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\:{Hence},\:{the}\:{radius} \\ $$$${of}\:{the}\:{circle}\:{in}\:{question}\:{is}\:{r}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}. \\ $$$${Using}\:{area},{A}=\pi{r}^{\mathrm{2}} \Rightarrow{A}=\frac{\mathrm{3}\pi}{\mathrm{4}}\:{square}\:{units}. \\ $$

Commented by Rasheed Soomro last updated on 05/May/16

Th^α nkS! I am trying to understand! I think that circle on a sphere is concave surface.. ..Anyway I like your approach very much. Not only in this answer but I always like your approach!

$$\mathbb{T}\boldsymbol{\mathrm{h}}^{\alpha} \boldsymbol{\mathrm{n}}\Bbbk\boldsymbol{\mathrm{S}}!\:\mathrm{I}\:\mathrm{am}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{understand}! \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{that}\:\mathrm{circle}\:\mathrm{on}\:\mathrm{a}\:\mathrm{sphere}\:\mathrm{is} \\ $$$$\mathrm{concave}\:\mathrm{surface}..\:..\mathrm{Anyway}\:\mathrm{I}\:\mathrm{like}\:\mathrm{your} \\ $$$$\mathrm{approach}\:\mathrm{very}\:\mathrm{much}.\:\mathrm{Not}\:\mathrm{only}\:\mathrm{in}\:\mathrm{this} \\ $$$$\mathrm{answer}\:\mathrm{but}\:\mathrm{I}\:\boldsymbol{\mathrm{always}}\:\:\mathrm{like}\:\mathrm{your}\:\mathrm{approach}! \\ $$

Commented by Yozzii last updated on 05/May/16

Ah yes. Thats a section of the surface of the sphere. Integral Calculus can easily derive the surface area given the central angle. You′d thus have to inregrate the function y=(√(1−x^2 )) between 0.5≤x≤1 using S=∫_(0.5) ^1 2πy(√(1+((dy/dx))^2 ))dx. That section,the cross−section of the sphere, defined by x^2 +y^2 =1 and 0.5≤x≤1 is rotated 2π radians about the x−axis. The geometry that I have outlined is what helps us find the lower limit of x=0.5.

$${Ah}\:{yes}.\:{Thats}\:{a}\:{section}\:{of}\:{the}\:{surface} \\ $$$${of}\:{the}\:{sphere}.\:{Integral}\:{Calculus}\:{can}\:{easily} \\ $$$${derive}\:{the}\:{surface}\:{area}\:{given}\:{the} \\ $$$${central}\:{angle}.\:{You}'{d}\:{thus}\:{have}\:{to} \\ $$$${inregrate}\:{the}\:{function}\:{y}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${between}\:\mathrm{0}.\mathrm{5}\leqslant{x}\leqslant\mathrm{1}\:{using} \\ $$$${S}=\int_{\mathrm{0}.\mathrm{5}} ^{\mathrm{1}} \mathrm{2}\pi{y}\sqrt{\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} }{dx}. \\ $$$${That}\:{section},{the}\:{cross}−{section} \\ $$$${of}\:{the}\:{sphere},\:{defined}\:{by}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$${and}\:\mathrm{0}.\mathrm{5}\leqslant{x}\leqslant\mathrm{1}\:{is}\:{rotated}\:\mathrm{2}\pi\:{radians} \\ $$$${about}\:{the}\:{x}−{axis}.\:{The}\:{geometry}\:{that}\:{I}\:{have} \\ $$$${outlined}\:{is}\:{what}\:{helps}\:{us}\:{find}\:{the} \\ $$$${lower}\:{limit}\:{of}\:{x}=\mathrm{0}.\mathrm{5}. \\ $$

Commented by Yozzii last updated on 05/May/16

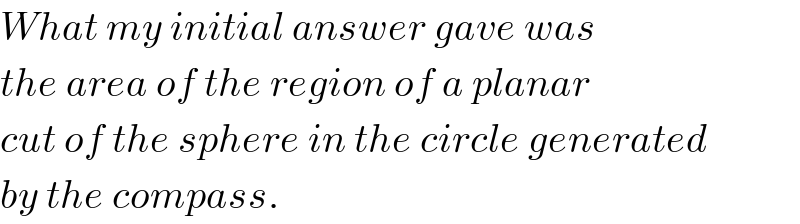
What my initial answer gave was the area of the region of a planar cut of the sphere in the circle generated by the compass.

$${What}\:{my}\:{initial}\:{answer}\:{gave}\:{was} \\ $$$${the}\:{area}\:{of}\:{the}\:{region}\:{of}\:{a}\:{planar} \\ $$$${cut}\:{of}\:{the}\:{sphere}\:{in}\:{the}\:{circle}\:{generated} \\ $$$${by}\:{the}\:{compass}. \\ $$

Commented by Rasheed Soomro last updated on 05/May/16

ThankS again!

$$\boldsymbol{\mathrm{ThankS}}\:\boldsymbol{\mathrm{again}}! \\ $$

Commented by Yozzii last updated on 05/May/16

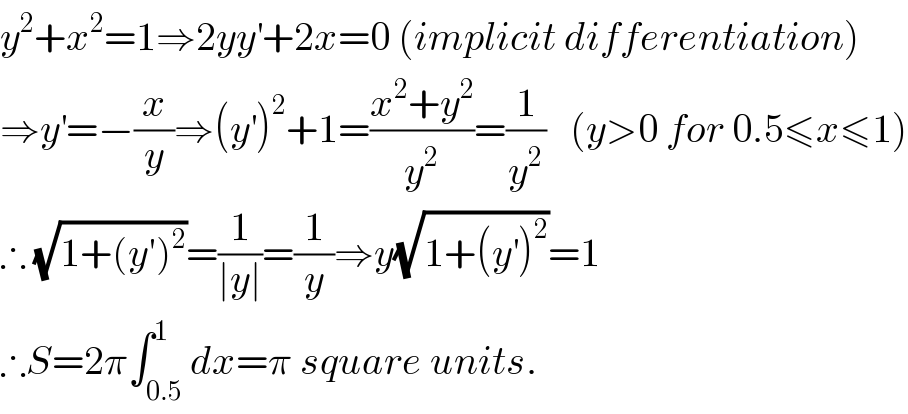
y^2 +x^2 =1⇒2yy^′ +2x=0 (implicit differentiation) ⇒y^′ =−(x/y)⇒(y^′ )^2 +1=((x^2 +y^2 )/y^2 )=(1/y^2 ) (y>0 for 0.5≤x≤1) ∴ (√(1+(y′)^2 ))=(1/(∣y∣))=(1/y)⇒y(√(1+(y^′ )^2 ))=1 ∴S=2π∫_(0.5) ^1 dx=π square units.

$${y}^{\mathrm{2}} +{x}^{\mathrm{2}} =\mathrm{1}\Rightarrow\mathrm{2}{yy}^{'} +\mathrm{2}{x}=\mathrm{0}\:\left({implicit}\:{differentiation}\right) \\ $$$$\Rightarrow{y}^{'} =−\frac{{x}}{{y}}\Rightarrow\left({y}^{'} \right)^{\mathrm{2}} +\mathrm{1}=\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{{y}^{\mathrm{2}} }=\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\:\:\:\left({y}>\mathrm{0}\:{for}\:\mathrm{0}.\mathrm{5}\leqslant{x}\leqslant\mathrm{1}\right) \\ $$$$\therefore\:\sqrt{\mathrm{1}+\left({y}'\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mid{y}\mid}=\frac{\mathrm{1}}{{y}}\Rightarrow{y}\sqrt{\mathrm{1}+\left({y}^{'} \right)^{\mathrm{2}} }=\mathrm{1} \\ $$$$\therefore{S}=\mathrm{2}\pi\int_{\mathrm{0}.\mathrm{5}} ^{\mathrm{1}} {dx}=\pi\:{square}\:{units}. \\ $$

Commented by Yozzii last updated on 05/May/16

Archimedes′ tombstone theorem is applicable here. So the required surface area, after finding that ∣JB∣=0.5, Area of surface of sphere between J and B equals the surface area of the surface, between two parallel planes containing the portion of sphere, of a cylinder circumscribing the entire sphere in question ∴ S=2πrh where r=radius of entire sphere h=∣BJ∣=0.5 ⇒S=2π×1×0.5=π square units as was found by integral calculus. The Pappus−Guldin theorem gives an alternative but perhaps longer method since the y coordinate of the cetroid of the region bounded by x=0.5,x=1, y=0 and x^2 +y^2 =1 needs to be found. ⇒ S=2πy^� s_0 where s_0 =arc length of y=rθ=1×(π/3)=(π/3) units, for 0.5≤x≤1.

$${Archimedes}'\:{tombstone}\:{theorem}\:{is} \\ $$$${applicable}\:{here}.\:{So}\:{the}\:{required}\:{surface} \\ $$$${area},\:{after}\:{finding}\:{that}\:\mid{JB}\mid=\mathrm{0}.\mathrm{5}, \\ $$$${Area}\:{of}\:{surface}\:{of}\:{sphere}\:{between}\:{J}\:{and}\:{B} \\ $$$${equals}\:{the}\:{surface}\:{area}\:{of}\:{the}\:{surface},\:{between} \\ $$$${two}\:{parallel}\:{planes}\:{containing}\:{the}\:{portion}\:{of}\:{sphere},\:{of} \\ $$$${a}\:{cylinder}\:{circumscribing}\:{the}\:{entire} \\ $$$${sphere}\:{in}\:{question} \\ $$$$\therefore\:{S}=\mathrm{2}\pi{rh} \\ $$$${where}\:{r}={radius}\:{of}\:{entire}\:{sphere} \\ $$$${h}=\mid{BJ}\mid=\mathrm{0}.\mathrm{5} \\ $$$$\Rightarrow{S}=\mathrm{2}\pi×\mathrm{1}×\mathrm{0}.\mathrm{5}=\pi\:{square}\:{units}\:{as}\:{was}\:{found} \\ $$$${by}\:{integral}\:{calculus}.\: \\ $$$${The}\:{Pappus}−{Guldin}\:{theorem}\:{gives} \\ $$$${an}\:{alternative}\:{but}\:{perhaps}\:{longer}\: \\ $$$${method}\:{since}\:{the}\:{y}\:{coordinate}\:{of}\:{the}\:{cetroid}\:{of}\:{the}\:{region} \\ $$$${bounded}\:{by}\:{x}=\mathrm{0}.\mathrm{5},{x}=\mathrm{1},\:{y}=\mathrm{0}\:{and} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}\:{needs}\:{to}\:{be}\:{found}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:{S}=\mathrm{2}\pi\bar {{y}s}_{\mathrm{0}} \\ $$$${where}\:{s}_{\mathrm{0}} ={arc}\:{length}\:{of}\:{y}={r}\theta=\mathrm{1}×\frac{\pi}{\mathrm{3}}=\frac{\pi}{\mathrm{3}}\:{units}, \\ $$$${for}\:\mathrm{0}.\mathrm{5}\leqslant{x}\leqslant\mathrm{1}. \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 06/May/16

LOT OF Knowledge! LOT OF ThankS!

$$\mathbb{LOT}\:\mathcal{OF}\:\mathrm{Knowledge}! \\ $$$$\mathbb{LOT}\:\mathcal{OF}\:\:\mathbb{T}\mathrm{han}\Bbbk\mathcal{S}! \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com