
Question Number 209432 by Tawa11 last updated on 10/Jul/24

A body is projected vertically upwards with a speed of 20m/s. Find the time in seconds when the body is 15m above it point of projection. g= 10m/s²
Answered by A5T last updated on 10/Jul/24
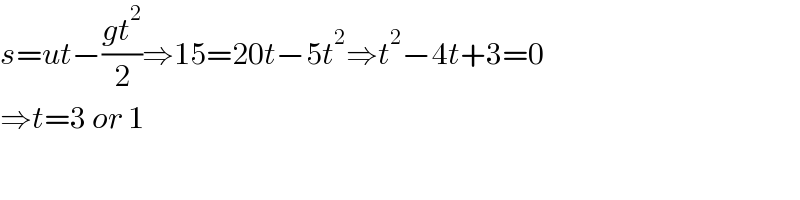
$${s}={ut}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}\Rightarrow\mathrm{15}=\mathrm{20}{t}−\mathrm{5}{t}^{\mathrm{2}} \Rightarrow{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{3}\:{or}\:\mathrm{1} \\ $$
Commented by Tawa11 last updated on 10/Jul/24
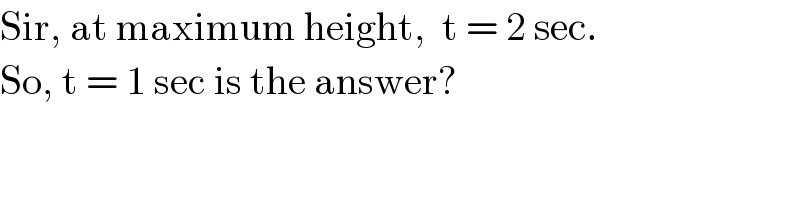
$$\mathrm{Sir},\:\mathrm{at}\:\mathrm{maximum}\:\mathrm{height},\:\:\mathrm{t}\:=\:\mathrm{2}\:\mathrm{sec}. \\ $$$$\mathrm{So},\:\mathrm{t}\:=\:\mathrm{1}\:\mathrm{sec}\:\mathrm{is}\:\mathrm{the}\:\mathrm{answer}? \\ $$
Commented by A5T last updated on 10/Jul/24
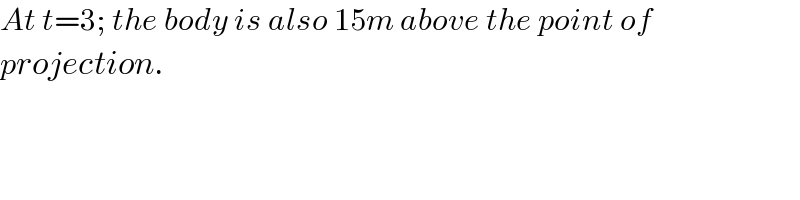
$${At}\:{t}=\mathrm{3};\:{the}\:{body}\:{is}\:{also}\:\mathrm{15}{m}\:{above}\:{the}\:{point}\:{of} \\ $$$${projection}. \\ $$
Commented by Tawa11 last updated on 10/Jul/24
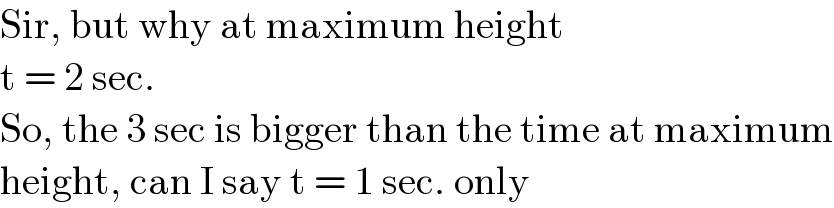
$$\mathrm{Sir},\:\mathrm{but}\:\mathrm{why}\:\mathrm{at}\:\mathrm{maximum}\:\mathrm{height} \\ $$$$\mathrm{t}\:=\:\mathrm{2}\:\mathrm{sec}. \\ $$$$\mathrm{So},\:\mathrm{the}\:\mathrm{3}\:\mathrm{sec}\:\mathrm{is}\:\mathrm{bigger}\:\mathrm{than}\:\mathrm{the}\:\mathrm{time}\:\mathrm{at}\:\mathrm{maximum} \\ $$$$\mathrm{height},\:\mathrm{can}\:\mathrm{I}\:\mathrm{say}\:\mathrm{t}\:=\:\mathrm{1}\:\mathrm{sec}.\:\mathrm{only} \\ $$
Commented by A5T last updated on 10/Jul/24

$${If}\:{we}\:{are}\:{considering}\:{the}\:{whole}\:{motion},\:{after} \\ $$$${t}=\mathrm{2}\:{the}\:{body}\:{will}\:{start}\:{to}\:{drop}\:{down}\:{from}\:\mathrm{20}{m}. \\ $$
Commented by Tawa11 last updated on 10/Jul/24

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{understand} \\ $$
Commented by Tawa11 last updated on 10/Jul/24

$$\mathrm{sir}\:\mathrm{help}\:\mathrm{me}\:\mathrm{check}\:\mathrm{Q209430} \\ $$
