Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 212456 by Hanuda354 last updated on 14/Oct/24

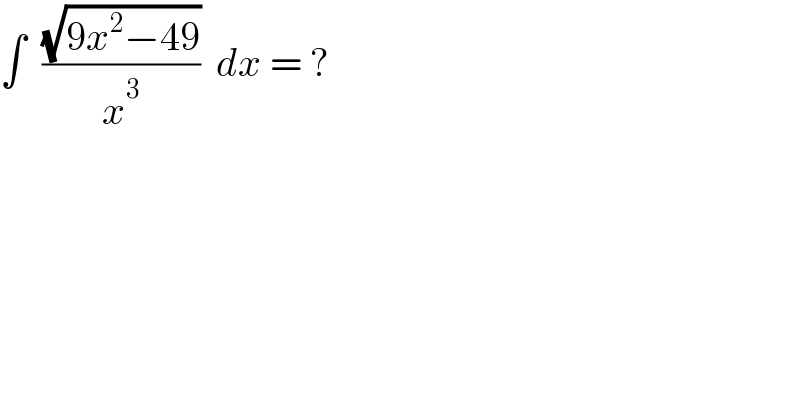
∫ ((√(9x^2 −49))/x^3 ) dx = ?

$$\int\:\:\frac{\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{49}}}{{x}^{\mathrm{3}} }\:\:{dx}\:=\:? \\ $$

Answered by Sutrisno last updated on 14/Oct/24

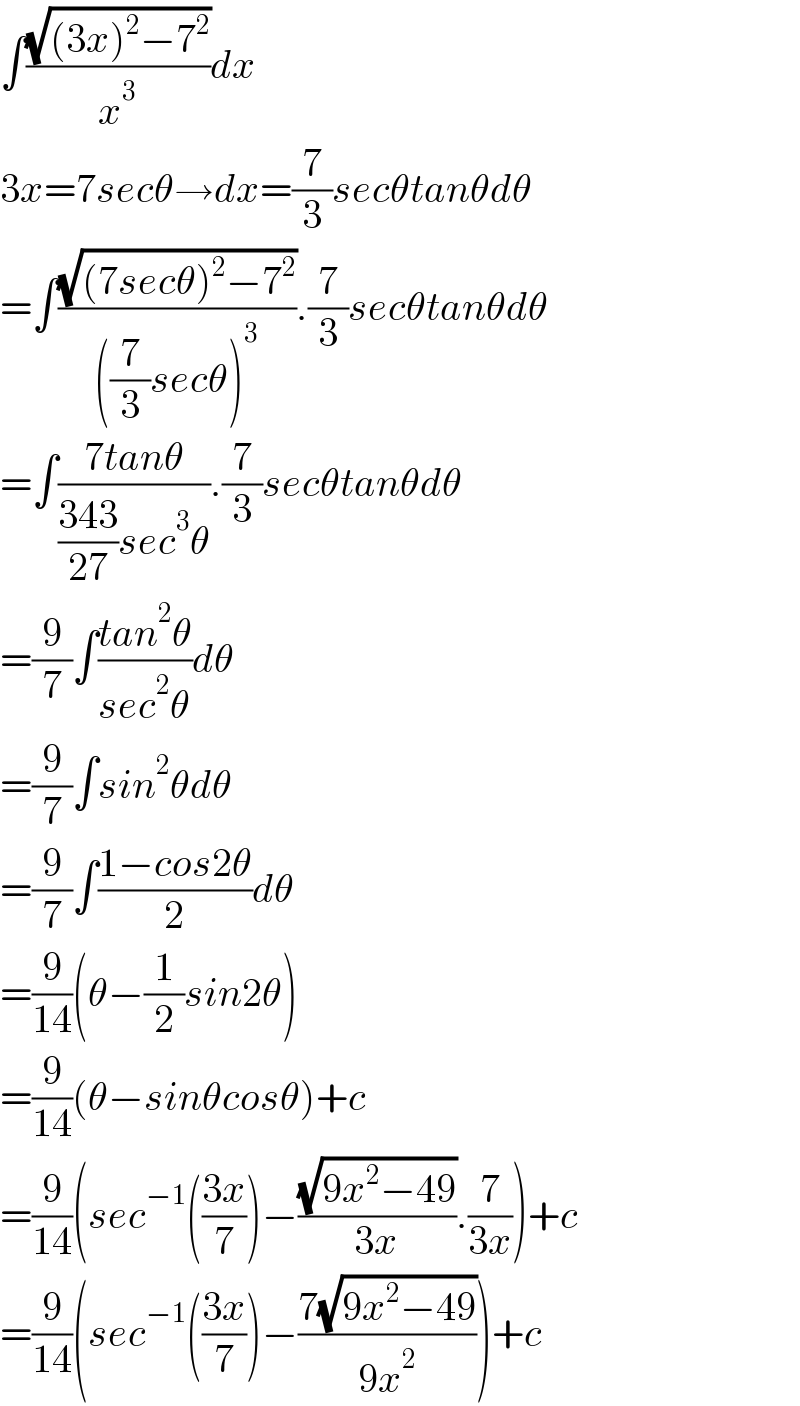
∫((√((3x)^2 −7^2 ))/x^3 )dx 3x=7secθ→dx=(7/3)secθtanθdθ =∫((√((7secθ)^2 −7^2 ))/(((7/3)secθ)^3 )).(7/3)secθtanθdθ =∫((7tanθ)/(((343)/(27))sec^3 θ)).(7/3)secθtanθdθ =(9/7)∫((tan^2 θ)/(sec^2 θ))dθ =(9/7)∫sin^2 θdθ =(9/7)∫((1−cos2θ)/2)dθ =(9/(14))(θ−(1/2)sin2θ) =(9/(14))(θ−sinθcosθ)+c =(9/(14))(sec^(−1) (((3x)/7))−((√(9x^2 −49))/(3x)).(7/(3x)))+c =(9/(14))(sec^(−1) (((3x)/7))−((7(√(9x^2 −49)))/(9x^2 )))+c

$$\int\frac{\sqrt{\left(\mathrm{3}{x}\right)^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }}{{x}^{\mathrm{3}} }{dx} \\ $$$$\mathrm{3}{x}=\mathrm{7}{sec}\theta\rightarrow{dx}=\frac{\mathrm{7}}{\mathrm{3}}{sec}\theta{tan}\theta{d}\theta \\ $$$$=\int\frac{\sqrt{\left(\mathrm{7}{sec}\theta\right)^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }}{\left(\frac{\mathrm{7}}{\mathrm{3}}{sec}\theta\right)^{\mathrm{3}} }.\frac{\mathrm{7}}{\mathrm{3}}{sec}\theta{tan}\theta{d}\theta \\ $$$$=\int\frac{\mathrm{7}{tan}\theta}{\frac{\mathrm{343}}{\mathrm{27}}{sec}^{\mathrm{3}} \theta}.\frac{\mathrm{7}}{\mathrm{3}}{sec}\theta{tan}\theta{d}\theta \\ $$$$=\frac{\mathrm{9}}{\mathrm{7}}\int\frac{{tan}^{\mathrm{2}} \theta}{{sec}^{\mathrm{2}} \theta}{d}\theta \\ $$$$=\frac{\mathrm{9}}{\mathrm{7}}\int{sin}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\frac{\mathrm{9}}{\mathrm{7}}\int\frac{\mathrm{1}−{cos}\mathrm{2}\theta}{\mathrm{2}}{d}\theta \\ $$$$=\frac{\mathrm{9}}{\mathrm{14}}\left(\theta−\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}\theta\right) \\ $$$$=\frac{\mathrm{9}}{\mathrm{14}}\left(\theta−{sin}\theta{cos}\theta\right)+{c} \\ $$$$=\frac{\mathrm{9}}{\mathrm{14}}\left({sec}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}}{\mathrm{7}}\right)−\frac{\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{49}}}{\mathrm{3}{x}}.\frac{\mathrm{7}}{\mathrm{3}{x}}\right)+{c} \\ $$$$=\frac{\mathrm{9}}{\mathrm{14}}\left({sec}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}}{\mathrm{7}}\right)−\frac{\mathrm{7}\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{49}}}{\mathrm{9}{x}^{\mathrm{2}} }\right)+{c} \\ $$

Commented by Hanuda354 last updated on 14/Oct/24

Thanks

$$\mathrm{Thanks} \\ $$

Answered by Ghisom last updated on 14/Oct/24

∫ ((√(9x^2 −49))/x^3 )dx= [t=arcsin ((14(√(9x^2 −49)))/x^2 ) → dx=−((x(√(9x^2 −49)))/(14))dt] =−(9/(28))∫(1+cos t)dt=−(9/(28))(t+sin t)= =−((√(9x^2 −49))/(2x^2 ))−(9/(28))arcsin ((14(√(9x^2 −49)))/x^2 ) +C

$$\int\:\frac{\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{49}}}{{x}^{\mathrm{3}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsin}\:\frac{\mathrm{14}\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{49}}}{{x}^{\mathrm{2}} }\:\rightarrow\:{dx}=−\frac{{x}\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{49}}}{\mathrm{14}}{dt}\right] \\ $$$$=−\frac{\mathrm{9}}{\mathrm{28}}\int\left(\mathrm{1}+\mathrm{cos}\:{t}\right){dt}=−\frac{\mathrm{9}}{\mathrm{28}}\left({t}+\mathrm{sin}\:{t}\right)= \\ $$$$=−\frac{\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{49}}}{\mathrm{2}{x}^{\mathrm{2}} }−\frac{\mathrm{9}}{\mathrm{28}}\mathrm{arcsin}\:\frac{\mathrm{14}\sqrt{\mathrm{9}{x}^{\mathrm{2}} −\mathrm{49}}}{{x}^{\mathrm{2}} }\:+{C} \\ $$

Commented by Hanuda354 last updated on 14/Oct/24

Thank you

$$\mathrm{Thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com