
Question Number 99960 by bemath last updated on 24/Jun/20
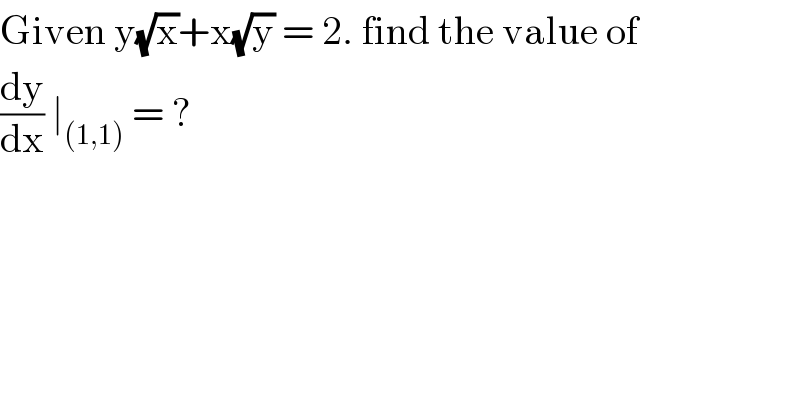
$$\mathrm{Given}\:\mathrm{y}\sqrt{\mathrm{x}}+\mathrm{x}\sqrt{\mathrm{y}}\:=\:\mathrm{2}.\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:\mid_{\left(\mathrm{1},\mathrm{1}\right)} \:=\:?\: \\ $$
Commented by Dwaipayan Shikari last updated on 24/Jun/20

$$−\mathrm{1} \\ $$
Answered by Rio Michael last updated on 24/Jun/20
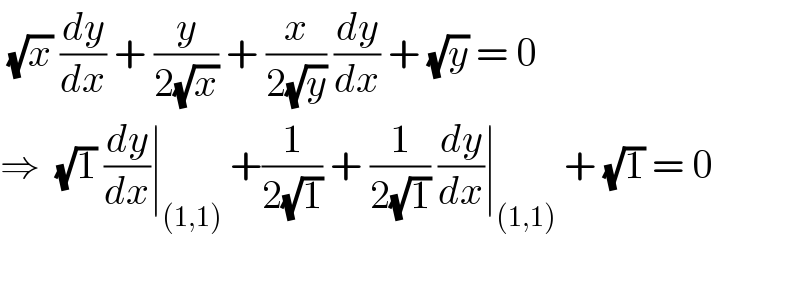
$$\:\sqrt{{x}}\:\frac{{dy}}{{dx}}\:+\:\frac{{y}}{\mathrm{2}\sqrt{{x}}}\:+\:\frac{{x}}{\mathrm{2}\sqrt{{y}}}\:\frac{{dy}}{{dx}}\:+\:\sqrt{{y}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\sqrt{\mathrm{1}}\:\frac{{dy}}{{dx}}\mid_{\left(\mathrm{1},\mathrm{1}\right)} \:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}}}\:+\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}}}\:\frac{{dy}}{{dx}}\mid_{\left(\mathrm{1},\mathrm{1}\right)} \:+\:\sqrt{\mathrm{1}}\:=\:\mathrm{0} \\ $$$$ \\ $$
Answered by 1549442205 last updated on 24/Jun/20
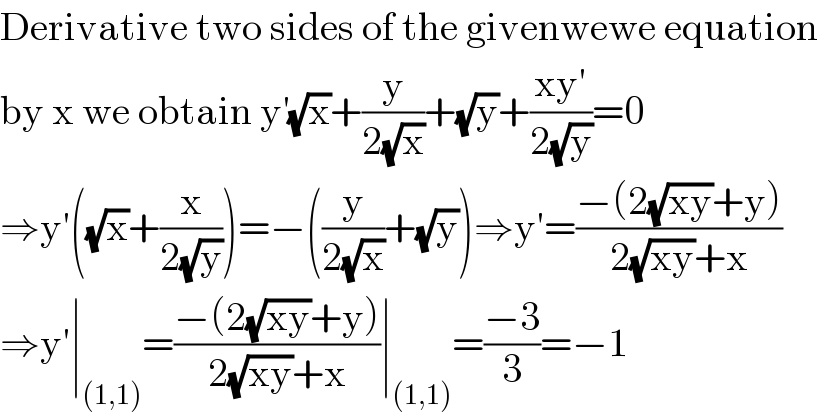
$$\mathrm{Derivative}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{the}\:\mathrm{givenwewe}\:\mathrm{equation} \\ $$$$\mathrm{by}\:\mathrm{x}\:\mathrm{we}\:\mathrm{obtain}\:\mathrm{y}^{'} \sqrt{\mathrm{x}}+\frac{\mathrm{y}}{\mathrm{2}\sqrt{\mathrm{x}}}+\sqrt{\mathrm{y}}+\frac{\mathrm{xy}'}{\mathrm{2}\sqrt{\mathrm{y}}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{y}'\left(\sqrt{\mathrm{x}}+\frac{\mathrm{x}}{\mathrm{2}\sqrt{\mathrm{y}}}\right)=−\left(\frac{\mathrm{y}}{\mathrm{2}\sqrt{\mathrm{x}}}+\sqrt{\mathrm{y}}\right)\Rightarrow\mathrm{y}'=\frac{−\left(\mathrm{2}\sqrt{\mathrm{xy}}+\mathrm{y}\right)}{\mathrm{2}\sqrt{\mathrm{xy}}+\mathrm{x}} \\ $$$$\Rightarrow\mathrm{y}'\mid_{\left(\mathrm{1},\mathrm{1}\right)} =\frac{−\left(\mathrm{2}\sqrt{\mathrm{xy}}+\mathrm{y}\right)}{\mathrm{2}\sqrt{\mathrm{xy}}+\mathrm{x}}\mid_{\left(\mathrm{1},\mathrm{1}\right)} =\frac{−\mathrm{3}}{\mathrm{3}}=−\mathrm{1} \\ $$
