
Question Number 99485 by Dwaipayan Shikari last updated on 21/Jun/20

$$\int{tan}^{\frac{\mathrm{1}}{\mathrm{5}}} {xdx} \\ $$
Answered by MJS last updated on 21/Jun/20
![t=tan^(2/5) x ∫tan^(1/5) x dx= [t=tan^(2/5) x → dx=(5/2)tan^(3/5) x cos^2 x dt] =(5/2)∫(t^2 /(t^5 +1))dt the rest is decomposing t^5 +1=(t+1)(t^2 −((1−(√5))/2)t+1)(t^2 −((1+(√5))/2)t+1)](Q99487.png)
$${t}=\mathrm{tan}^{\mathrm{2}/\mathrm{5}} \:{x} \\ $$$$\int\mathrm{tan}^{\mathrm{1}/\mathrm{5}} \:{x}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}^{\mathrm{2}/\mathrm{5}} \:{x}\:\rightarrow\:{dx}=\frac{\mathrm{5}}{\mathrm{2}}\mathrm{tan}^{\mathrm{3}/\mathrm{5}} \:{x}\:\mathrm{cos}^{\mathrm{2}} \:{x}\:\mathrm{dt}\right] \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}\int\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{5}} +\mathrm{1}}{dt} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{decomposing} \\ $$$${t}^{\mathrm{5}} +\mathrm{1}=\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{t}+\mathrm{1}\right) \\ $$
Commented by PRITHWISH SEN 2 last updated on 21/Jun/20

$$\mathrm{the}\:\mathrm{decomosition} \\ $$$$−\frac{\mathrm{2}\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}\:\left(\mathrm{1}+\mathrm{t}^{\mathrm{5}} \right)}{\mathrm{5}\left\{\mathrm{2t}^{\mathrm{2}} +\mathrm{2t}^{\mathrm{3}} −\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}\:\mathrm{t}^{\frac{\mathrm{5}}{\mathrm{2}}} \right\}}\:+\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}\left(\mathrm{1}+\mathrm{t}^{\mathrm{5}} \right)}{\mathrm{20}\left\{\mathrm{2t}^{\mathrm{2}} +\mathrm{2t}^{\mathrm{3}} −\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}\:\mathrm{t}^{\frac{\mathrm{5}}{\mathrm{2}}} \right.} \\ $$$$+\frac{\mathrm{2}\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}\left(\mathrm{1}+\mathrm{t}^{\mathrm{5}} \right)}{\left\{\mathrm{2t}^{\mathrm{2}} +\mathrm{2t}^{\mathrm{3}} +\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}\:\mathrm{t}^{\frac{\mathrm{5}}{\mathrm{2}}} \right\}}\:+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}\left(\mathrm{1}+\mathrm{t}^{\mathrm{5}} \right)}{\mathrm{20}\left\{\mathrm{2t}^{\mathrm{2}} +\mathrm{2t}^{\mathrm{3}} +\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}\:\mathrm{t}^{\frac{\mathrm{5}}{\mathrm{2}}} \right\}}\:+ \\ $$$$\:\:\:\:\frac{\left(\mathrm{1}+\mathrm{t}^{\mathrm{5}} \right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{t}\right)\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:−\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{5}} \right)^{\mathrm{2}} }{\mathrm{40}\left\{\mathrm{t}+\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}}}\:\sqrt{\mathrm{t}}\:+\mathrm{1}\right\}}\: \\ $$$$\:\:\:\:\:\:−\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{5}} \right)^{\mathrm{2}} }{\mathrm{40}\left\{\mathrm{t}−\sqrt{\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}}}\:\sqrt{\mathrm{t}}+\mathrm{1}\right\}}\:+ \\ $$$$\:\:\:\:\:\:\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{5}} \right)^{\mathrm{2}} }{\mathrm{40}\left\{\mathrm{t}+\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}}\:\sqrt{\mathrm{t}}+\mathrm{1}\right\}}\:\left\{\frac{\mathrm{2}}{\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:+\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}}\:.\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right\} \\ $$$$\:\:\: \\ $$$$\:+\:\:\:\:\:\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{5}} \right)^{\mathrm{2}} }{\mathrm{40}\left\{\mathrm{t}−\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}}\:\sqrt{\mathrm{t}}+\mathrm{1}\right\}}\:\left\{\frac{\mathrm{2}}{\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:−\sqrt{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}}\:.\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right\} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{I}}\:\:\boldsymbol{\mathrm{did}}\:\boldsymbol{\mathrm{not}}\:\boldsymbol{\mathrm{check}}\:\boldsymbol{\mathrm{it}}\:.\:\boldsymbol{\mathrm{Please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 21/Jun/20

Commented by PRITHWISH SEN 2 last updated on 21/Jun/20

$$\boldsymbol{\mathrm{from}}\:\boldsymbol{\mathrm{wolfram}}\:\boldsymbol{\mathrm{alpha}} \\ $$
Commented by MJS last updated on 21/Jun/20

$$\mathrm{that}'\mathrm{s}\:\mathrm{exactly}\:\mathrm{where}\:\mathrm{my}\:\mathrm{path}\:\mathrm{leads}\:\mathrm{to},\:\mathrm{no} \\ $$$$\mathrm{machine}\:\mathrm{logic}\:\mathrm{needed}.\:\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{horrible} \\ $$$$\mathrm{constants}\:\mathrm{once}\:\mathrm{again} \\ $$
Answered by maths mind last updated on 22/Jun/20
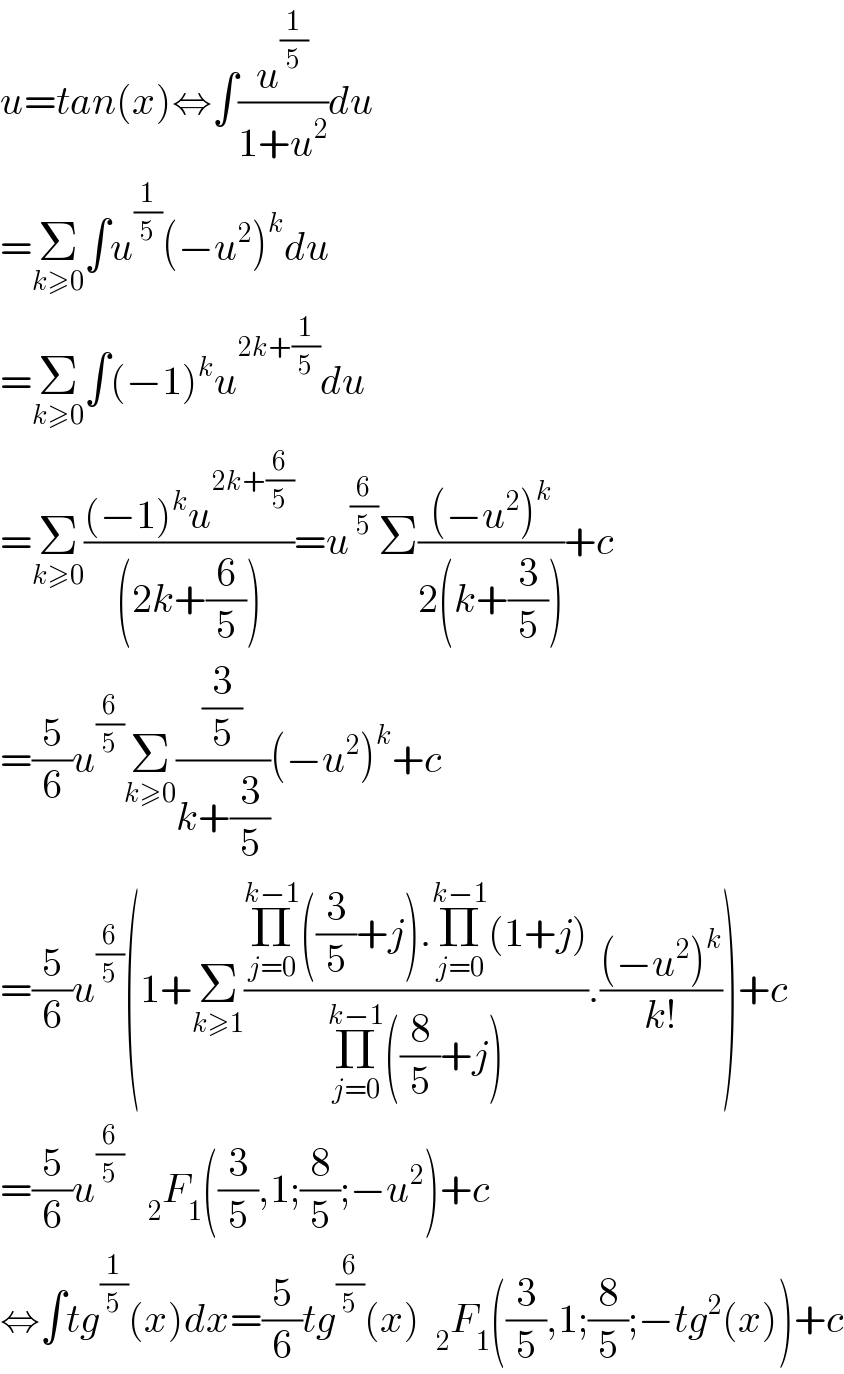
$${u}={tan}\left({x}\right)\Leftrightarrow\int\frac{{u}^{\frac{\mathrm{1}}{\mathrm{5}}} }{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\int{u}^{\frac{\mathrm{1}}{\mathrm{5}}} \left(−{u}^{\mathrm{2}} \right)^{{k}} {du} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\int\left(−\mathrm{1}\right)^{{k}} {u}^{\mathrm{2}{k}+\frac{\mathrm{1}}{\mathrm{5}}} {du} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {u}^{\mathrm{2}{k}+\frac{\mathrm{6}}{\mathrm{5}}} }{\left(\mathrm{2}{k}+\frac{\mathrm{6}}{\mathrm{5}}\right)}={u}^{\frac{\mathrm{6}}{\mathrm{5}}} \Sigma\frac{\left(−{u}^{\mathrm{2}} \right)^{{k}} }{\mathrm{2}\left({k}+\frac{\mathrm{3}}{\mathrm{5}}\right)}+{c} \\ $$$$=\frac{\mathrm{5}}{\mathrm{6}}{u}^{\frac{\mathrm{6}}{\mathrm{5}}} \underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\frac{\mathrm{3}}{\mathrm{5}}}{{k}+\frac{\mathrm{3}}{\mathrm{5}}}\left(−{u}^{\mathrm{2}} \right)^{{k}} +{c} \\ $$$$=\frac{\mathrm{5}}{\mathrm{6}}{u}^{\frac{\mathrm{6}}{\mathrm{5}}} \left(\mathrm{1}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\underset{{j}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left(\frac{\mathrm{3}}{\mathrm{5}}+{j}\right).\underset{{j}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left(\mathrm{1}+{j}\right)}{\underset{{j}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left(\frac{\mathrm{8}}{\mathrm{5}}+{j}\right)}.\frac{\left(−{u}^{\mathrm{2}} \right)^{{k}} }{{k}!}\right)+{c} \\ $$$$=\frac{\mathrm{5}}{\mathrm{6}}{u}^{\frac{\mathrm{6}}{\mathrm{5}}} \:\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{5}},\mathrm{1};\frac{\mathrm{8}}{\mathrm{5}};−{u}^{\mathrm{2}} \right)+{c} \\ $$$$\Leftrightarrow\int{tg}^{\frac{\mathrm{1}}{\mathrm{5}}} \left({x}\right){dx}=\frac{\mathrm{5}}{\mathrm{6}}{tg}^{\frac{\mathrm{6}}{\mathrm{5}}} \left({x}\right)\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{5}},\mathrm{1};\frac{\mathrm{8}}{\mathrm{5}};−{tg}^{\mathrm{2}} \left({x}\right)\right)+{c} \\ $$
