
Previous in Relation and Functions Next in Relation and Functions
Question Number 99463 by mathmax by abdo last updated on 21/Jun/20
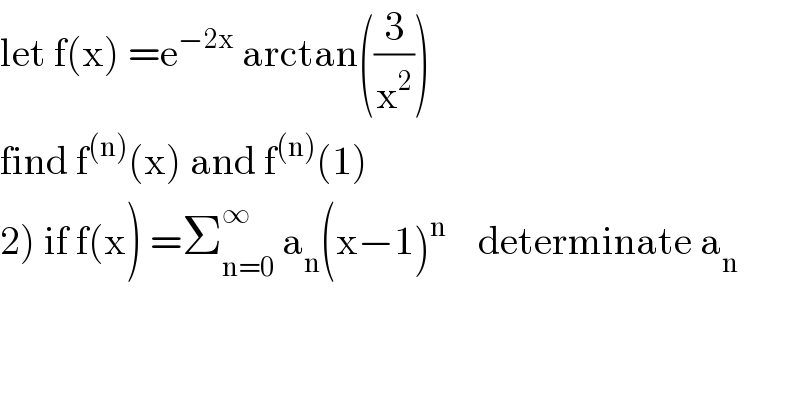
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{−\mathrm{2x}} \:\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }\right) \\ $$$$\mathrm{find}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{1}\right) \\ $$$$\left.\mathrm{2}\right)\:\mathrm{if}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{a}_{\mathrm{n}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{n}} \:\:\:\:\mathrm{determinate}\:\mathrm{a}_{\mathrm{n}} \\ $$
Answered by mathmax by abdo last updated on 23/Jun/20
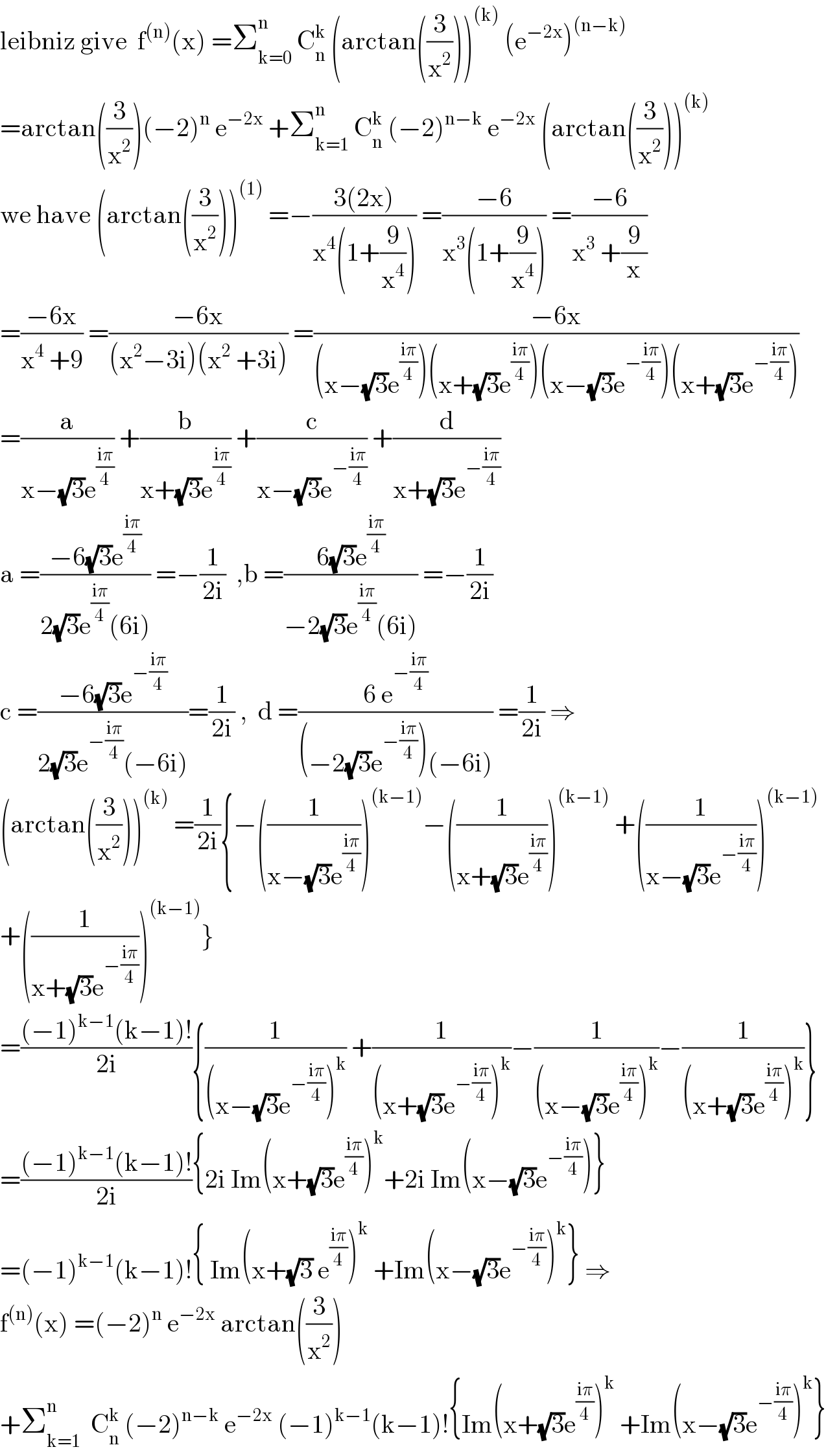
$$\mathrm{leibniz}\:\mathrm{give}\:\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }\right)\right)^{\left(\mathrm{k}\right)} \:\left(\mathrm{e}^{−\mathrm{2x}} \right)^{\left(\mathrm{n}−\mathrm{k}\right)} \\ $$$$=\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }\right)\left(−\mathrm{2}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{2x}} \:+\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}\:\:} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(−\mathrm{2}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{e}^{−\mathrm{2x}} \:\left(\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }\right)\right)^{\left(\mathrm{k}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\left(\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }\right)\right)^{\left(\mathrm{1}\right)} \:=−\frac{\mathrm{3}\left(\mathrm{2x}\right)}{\mathrm{x}^{\mathrm{4}} \left(\mathrm{1}+\frac{\mathrm{9}}{\mathrm{x}^{\mathrm{4}} }\right)}\:=\frac{−\mathrm{6}}{\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}+\frac{\mathrm{9}}{\mathrm{x}^{\mathrm{4}} }\right)}\:=\frac{−\mathrm{6}}{\mathrm{x}^{\mathrm{3}} \:+\frac{\mathrm{9}}{\mathrm{x}}} \\ $$$$=\frac{−\mathrm{6x}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{9}}\:=\frac{−\mathrm{6x}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3i}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{3i}\right)}\:=\frac{−\mathrm{6x}}{\left(\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{x}+\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{x}+\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \\ $$$$=\frac{\mathrm{a}}{\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }\:+\frac{\mathrm{b}}{\mathrm{x}+\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }\:+\frac{\mathrm{c}}{\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} }\:+\frac{\mathrm{d}}{\mathrm{x}+\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} } \\ $$$$\mathrm{a}\:=\frac{−\mathrm{6}\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }{\mathrm{2}\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(\mathrm{6i}\right)}\:=−\frac{\mathrm{1}}{\mathrm{2i}}\:\:,\mathrm{b}\:=\frac{\mathrm{6}\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }{−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(\mathrm{6i}\right)}\:=−\frac{\mathrm{1}}{\mathrm{2i}} \\ $$$$\mathrm{c}\:=\frac{−\mathrm{6}\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} }{\mathrm{2}\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(−\mathrm{6i}\right)}=\frac{\mathrm{1}}{\mathrm{2i}}\:,\:\:\mathrm{d}\:=\frac{\mathrm{6}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} }{\left(−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(−\mathrm{6i}\right)}\:=\frac{\mathrm{1}}{\mathrm{2i}}\:\Rightarrow \\ $$$$\left(\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }\right)\right)^{\left(\mathrm{k}\right)} \:=\frac{\mathrm{1}}{\mathrm{2i}}\left\{−\left(\frac{\mathrm{1}}{\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }\right)^{\left(\mathrm{k}−\mathrm{1}\right)} −\left(\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }\right)^{\left(\mathrm{k}−\mathrm{1}\right)} \:+\left(\frac{\mathrm{1}}{\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} }\right)^{\left(\mathrm{k}−\mathrm{1}\right)} \right. \\ $$$$\left.+\left(\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} }\right)^{\left(\mathrm{k}−\mathrm{1}\right)} \right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!}{\mathrm{2i}}\left\{\frac{\mathrm{1}}{\left(\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{k}} }\:+\frac{\mathrm{1}}{\left(\mathrm{x}+\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{k}} }−\frac{\mathrm{1}}{\left(\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{k}} }−\frac{\mathrm{1}}{\left(\mathrm{x}+\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{k}} }\right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!}{\mathrm{2i}}\left\{\mathrm{2i}\:\mathrm{Im}\left(\mathrm{x}+\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{k}} +\mathrm{2i}\:\mathrm{Im}\left(\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!\left\{\:\mathrm{Im}\left(\mathrm{x}+\sqrt{\mathrm{3}}\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{k}} \:+\mathrm{Im}\left(\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{k}} \right\}\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\left(−\mathrm{2}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }\right) \\ $$$$+\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\left(−\mathrm{2}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{e}^{−\mathrm{2x}} \:\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!\left\{\mathrm{Im}\left(\mathrm{x}+\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{k}} \:+\mathrm{Im}\left(\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)^{\mathrm{k}} \right\} \\ $$
