
Question Number 99045 by bobhans last updated on 18/Jun/20
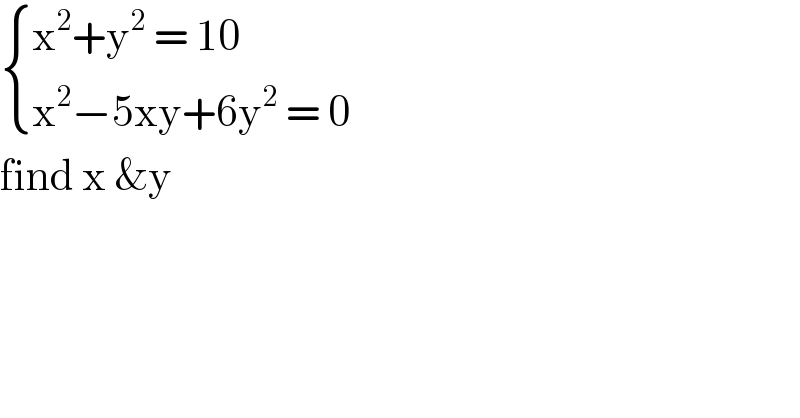
$$\begin{cases}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{10}}\\{\mathrm{x}^{\mathrm{2}} −\mathrm{5xy}+\mathrm{6y}^{\mathrm{2}} \:=\:\mathrm{0}}\end{cases} \\ $$ $$\mathrm{find}\:\mathrm{x}\:\&\mathrm{y}\: \\ $$
Answered by bemath last updated on 18/Jun/20
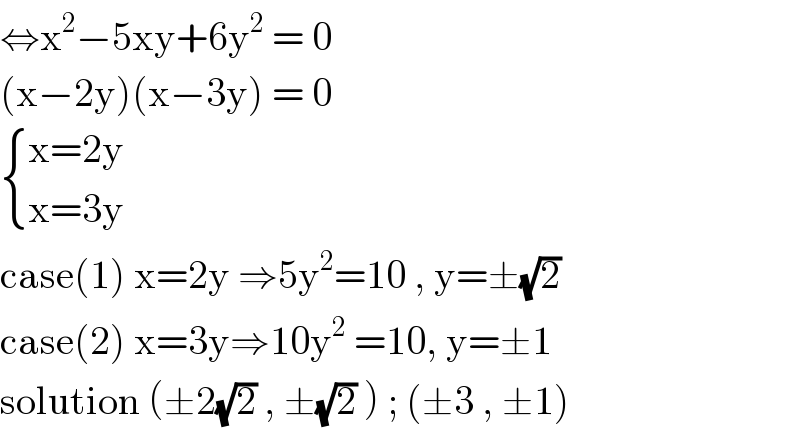
$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{5xy}+\mathrm{6y}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$ $$\left(\mathrm{x}−\mathrm{2y}\right)\left(\mathrm{x}−\mathrm{3y}\right)\:=\:\mathrm{0} \\ $$ $$\begin{cases}{\mathrm{x}=\mathrm{2y}}\\{\mathrm{x}=\mathrm{3y}}\end{cases} \\ $$ $$\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{x}=\mathrm{2y}\:\Rightarrow\mathrm{5y}^{\mathrm{2}} =\mathrm{10}\:,\:\mathrm{y}=\pm\sqrt{\mathrm{2}} \\ $$ $$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{x}=\mathrm{3y}\Rightarrow\mathrm{10y}^{\mathrm{2}} \:=\mathrm{10},\:\mathrm{y}=\pm\mathrm{1} \\ $$ $$\mathrm{solution}\:\left(\pm\mathrm{2}\sqrt{\mathrm{2}}\:,\:\pm\sqrt{\mathrm{2}}\:\right)\:;\:\left(\pm\mathrm{3}\:,\:\pm\mathrm{1}\right)\: \\ $$
