
Question Number 99007 by Rio Michael last updated on 18/Jun/20
) ) dy then I_y = ???](Q99007.png)
$$\mathrm{Let}\:{I}_{{y}} \:=\:\underset{−\mathrm{2}} {\overset{\mathrm{2}} {\int}}\left[{y}^{\mathrm{3}} \:\mathrm{cos}\:\left(\frac{{y}}{\mathrm{2}}\right)\:+\:\frac{\mathrm{1}}{\mathrm{2}}\right]\left(\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }\:\right)\:{dy}\: \\ $$$$\mathrm{then}\:{I}_{{y}} \:=\:??? \\ $$
Answered by maths mind last updated on 18/Jun/20
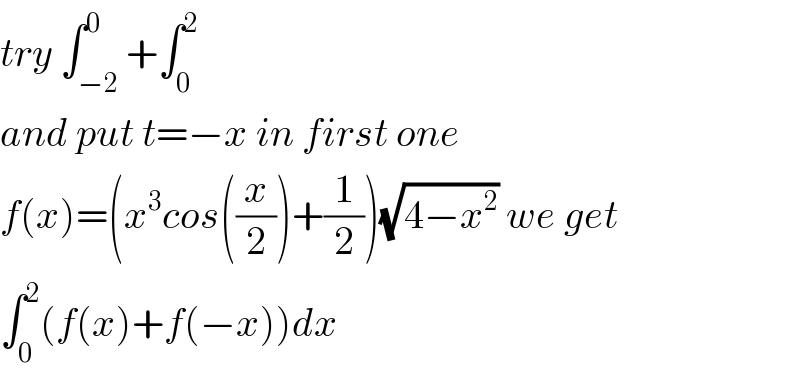
$${try}\:\int_{−\mathrm{2}} ^{\mathrm{0}} +\int_{\mathrm{0}} ^{\mathrm{2}} \\ $$$${and}\:{put}\:{t}=−{x}\:{in}\:{first}\:{one}\: \\ $$$${f}\left({x}\right)=\left({x}^{\mathrm{3}} {cos}\left(\frac{{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{we}\:{get} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \left({f}\left({x}\right)+{f}\left(−{x}\right)\right){dx} \\ $$
Commented by Rio Michael last updated on 18/Jun/20
$$\mathrm{Thanks}\:,\mathrm{i}\:\mathrm{solved}\:\mathrm{it}\:\mathrm{already}. \\ $$
Commented by maths mind last updated on 18/Jun/20
$${withe}\:{pleaser}\:{Nice}\:{sir} \\ $$
Answered by frc2crc last updated on 18/Jun/20
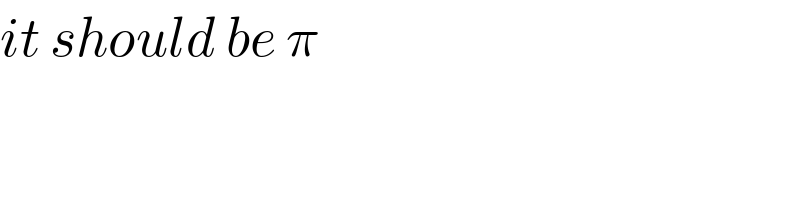
$${it}\:{should}\:{be}\:\pi \\ $$
