
Question Number 97412 by mr W last updated on 07/Jun/20
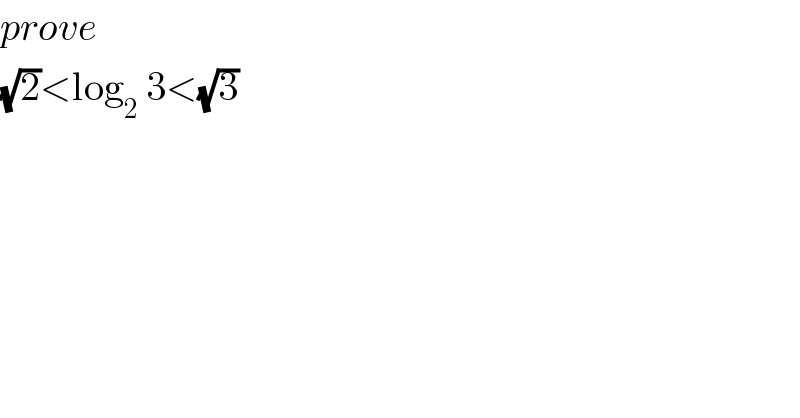
$${prove} \\ $$ $$\sqrt{\mathrm{2}}<\mathrm{log}_{\mathrm{2}} \:\mathrm{3}<\sqrt{\mathrm{3}} \\ $$
Answered by bobhans last updated on 08/Jun/20
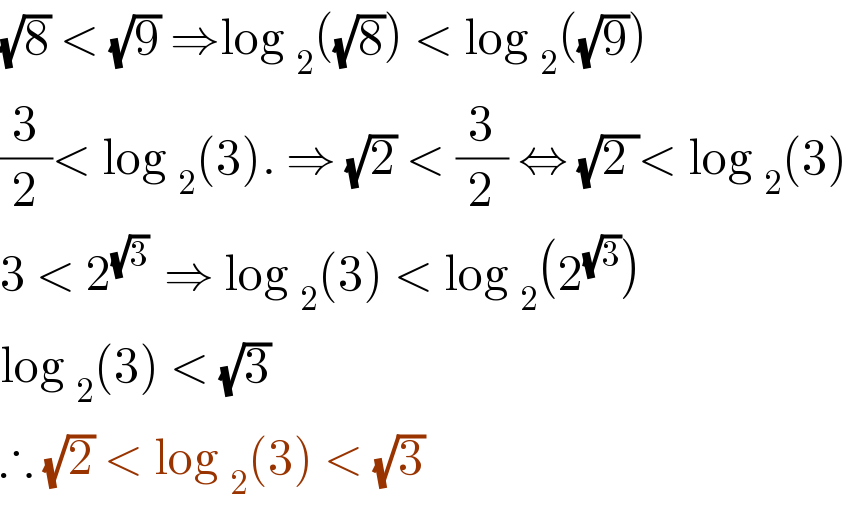
$$\sqrt{\mathrm{8}}\:<\:\sqrt{\mathrm{9}}\:\Rightarrow\mathrm{log}\:_{\mathrm{2}} \left(\sqrt{\mathrm{8}}\right)\:<\:\mathrm{log}\:_{\mathrm{2}} \left(\sqrt{\mathrm{9}}\right) \\ $$ $$\frac{\mathrm{3}}{\mathrm{2}}<\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right).\:\Rightarrow\:\sqrt{\mathrm{2}}\:<\:\frac{\mathrm{3}}{\mathrm{2}}\:\Leftrightarrow\:\sqrt{\mathrm{2}\:}<\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)\: \\ $$ $$\mathrm{3}\:<\:\mathrm{2}^{\sqrt{\mathrm{3}}\:} \:\Rightarrow\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)\:<\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{2}^{\sqrt{\mathrm{3}}} \right) \\ $$ $$\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)\:<\:\sqrt{\mathrm{3}}\: \\ $$ $$\therefore\:\sqrt{\mathrm{2}}\:<\:\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)\:<\:\sqrt{\mathrm{3}}\: \\ $$
Answered by 1549442205 last updated on 08/Jun/20
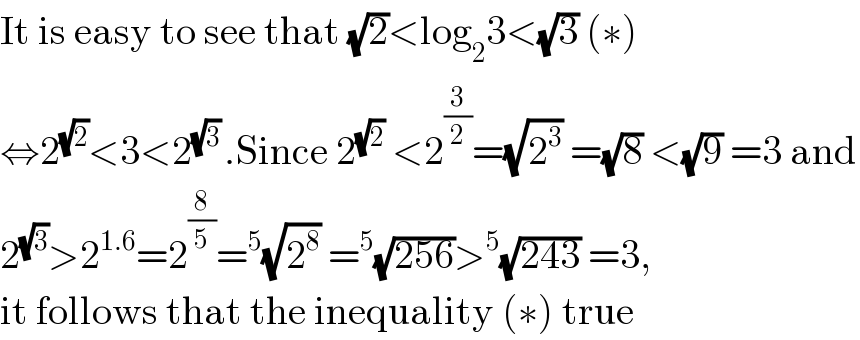
$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\sqrt{\mathrm{2}}<\mathrm{log}_{\mathrm{2}} \mathrm{3}<\sqrt{\mathrm{3}}\:\left(\ast\right) \\ $$ $$\Leftrightarrow\mathrm{2}^{\sqrt{\mathrm{2}}} <\mathrm{3}<\mathrm{2}^{\sqrt{\mathrm{3}}\:} .\mathrm{Since}\:\mathrm{2}^{\sqrt{\mathrm{2}}} \:<\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} =\sqrt{\mathrm{2}^{\mathrm{3}} }\:=\sqrt{\mathrm{8}}\:<\sqrt{\mathrm{9}}\:=\mathrm{3}\:\mathrm{and} \\ $$ $$\mathrm{2}^{\sqrt{\mathrm{3}}} >\mathrm{2}^{\mathrm{1}.\mathrm{6}} =\mathrm{2}^{\frac{\mathrm{8}}{\mathrm{5}}} =^{\mathrm{5}} \sqrt{\mathrm{2}^{\mathrm{8}} }\:=^{\mathrm{5}} \sqrt{\mathrm{256}}>^{\mathrm{5}} \sqrt{\mathrm{243}}\:=\mathrm{3}, \\ $$ $$\mathrm{it}\:\mathrm{follows}\:\mathrm{that}\:\mathrm{the}\:\mathrm{inequality}\:\left(\ast\right)\:\mathrm{true}\: \\ $$
