
Question Number 97368 by Riad last updated on 07/Jun/20
Commented by Tony Lin last updated on 07/Jun/20
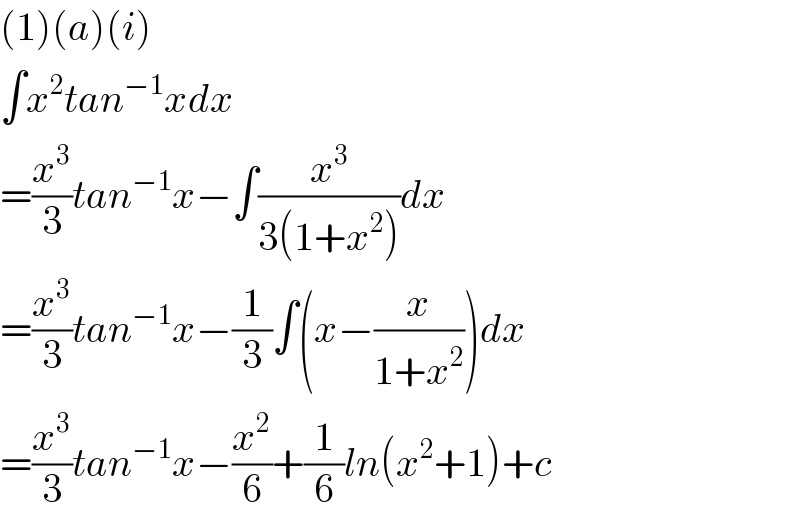
$$\left(\mathrm{1}\right)\left({a}\right)\left({i}\right) \\ $$$$\int{x}^{\mathrm{2}} {tan}^{−\mathrm{1}} {xdx} \\ $$$$=\frac{{x}^{\mathrm{3}} }{\mathrm{3}}{tan}^{−\mathrm{1}} {x}−\int\frac{{x}^{\mathrm{3}} }{\mathrm{3}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\frac{{x}^{\mathrm{3}} }{\mathrm{3}}{tan}^{−\mathrm{1}} {x}−\frac{\mathrm{1}}{\mathrm{3}}\int\left({x}−\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx} \\ $$$$=\frac{{x}^{\mathrm{3}} }{\mathrm{3}}{tan}^{−\mathrm{1}} {x}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{c} \\ $$
Commented by Riad last updated on 07/Jun/20

$${thanks} \\ $$
Commented by Tony Lin last updated on 07/Jun/20
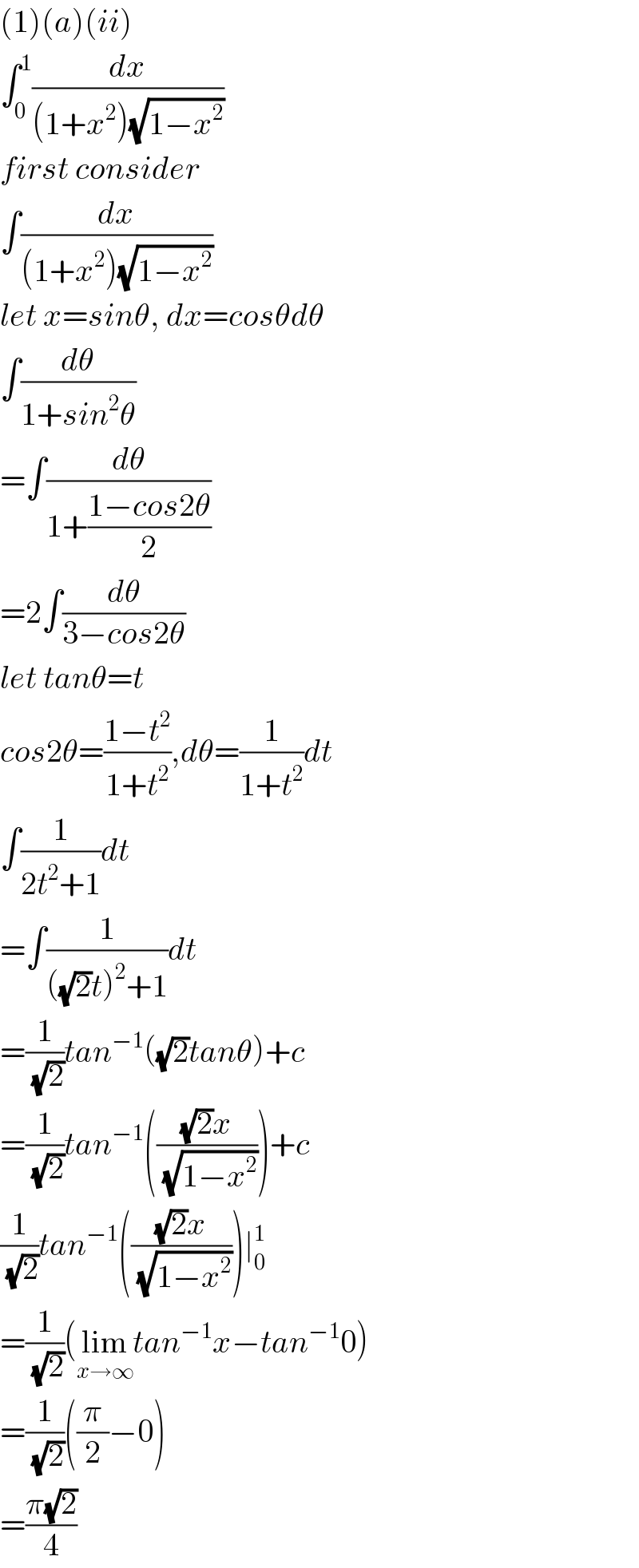
$$\left(\mathrm{1}\right)\left({a}\right)\left({ii}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${first}\:{consider} \\ $$$$\int\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${let}\:{x}={sin}\theta,\:{dx}={cos}\theta{d}\theta \\ $$$$\int\frac{{d}\theta}{\mathrm{1}+{sin}^{\mathrm{2}} \theta} \\ $$$$=\int\frac{{d}\theta}{\mathrm{1}+\frac{\mathrm{1}−{cos}\mathrm{2}\theta}{\mathrm{2}}} \\ $$$$=\mathrm{2}\int\frac{{d}\theta}{\mathrm{3}−{cos}\mathrm{2}\theta} \\ $$$${let}\:{tan}\theta={t} \\ $$$${cos}\mathrm{2}\theta=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} },{d}\theta=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$=\int\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}{t}\right)^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}{tan}\theta\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}}{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)+{c} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}}{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}{tan}^{−\mathrm{1}} {x}−{tan}^{−\mathrm{1}} \mathrm{0}\right) \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left(\frac{\pi}{\mathrm{2}}−\mathrm{0}\right) \\ $$$$=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$
Commented by Tony Lin last updated on 07/Jun/20
![(2)(a) u_x =(y^2 /(1+xy^2 )) u_y =((2xy)/(1+xy^2 )) u_(xx) =((−y^2 )/((1+xy^2 )^2 )) u_(yy) =((2x−2x^2 y^2 )/((1+xy^2 )^2 )) u_(xy) =((2y−2y^2 x^2 )/((1+y^2 x)^2 )) 2u_(xx) +u_(yy) +y^3 u_(xy) =−2[((y^2 −x+x^2 y^2 −y^4 +y^4 x^2 )/((1+y^2 x)^2 ))]](Q97391.png)
$$\left(\mathrm{2}\right)\left({a}\right) \\ $$$${u}_{{x}} =\frac{{y}^{\mathrm{2}} }{\mathrm{1}+{xy}^{\mathrm{2}} } \\ $$$${u}_{{y}} =\frac{\mathrm{2}{xy}}{\mathrm{1}+{xy}^{\mathrm{2}} } \\ $$$${u}_{{xx}} =\frac{−{y}^{\mathrm{2}} }{\left(\mathrm{1}+{xy}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${u}_{{yy}} =\frac{\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} }{\left(\mathrm{1}+{xy}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${u}_{{xy}} =\frac{\mathrm{2}{y}−\mathrm{2}{y}^{\mathrm{2}} {x}^{\mathrm{2}} }{\left(\mathrm{1}+{y}^{\mathrm{2}} {x}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}{u}_{{xx}} +{u}_{{yy}} +{y}^{\mathrm{3}} {u}_{{xy}} \\ $$$$=−\mathrm{2}\left[\frac{{y}^{\mathrm{2}} −{x}+{x}^{\mathrm{2}} {y}^{\mathrm{2}} −{y}^{\mathrm{4}} +{y}^{\mathrm{4}} {x}^{\mathrm{2}} }{\left(\mathrm{1}+{y}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }\right] \\ $$
Commented by Tony Lin last updated on 07/Jun/20
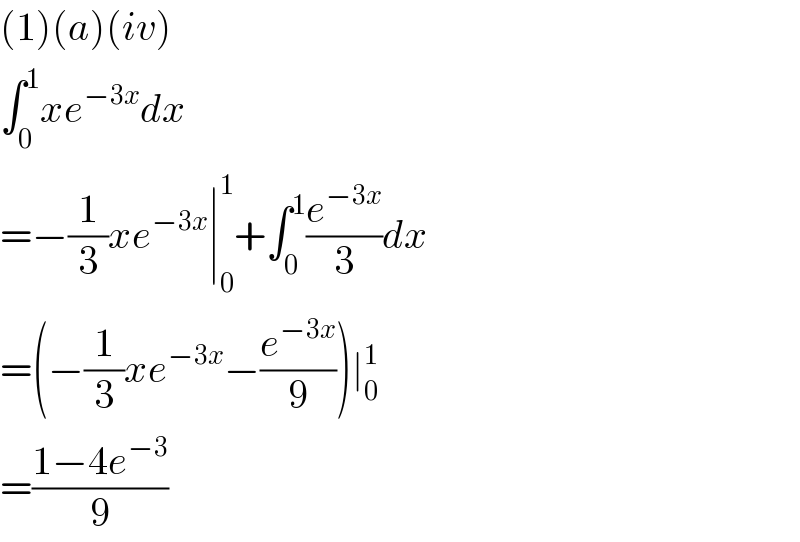
$$\left(\mathrm{1}\right)\left({a}\right)\left({iv}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {xe}^{−\mathrm{3}{x}} {dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}{xe}^{−\mathrm{3}{x}} \mid_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{e}^{−\mathrm{3}{x}} }{\mathrm{3}}{dx} \\ $$$$=\left(−\frac{\mathrm{1}}{\mathrm{3}}{xe}^{−\mathrm{3}{x}} −\frac{{e}^{−\mathrm{3}{x}} }{\mathrm{9}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}−\mathrm{4}{e}^{−\mathrm{3}} }{\mathrm{9}} \\ $$
Commented by Tony Lin last updated on 07/Jun/20
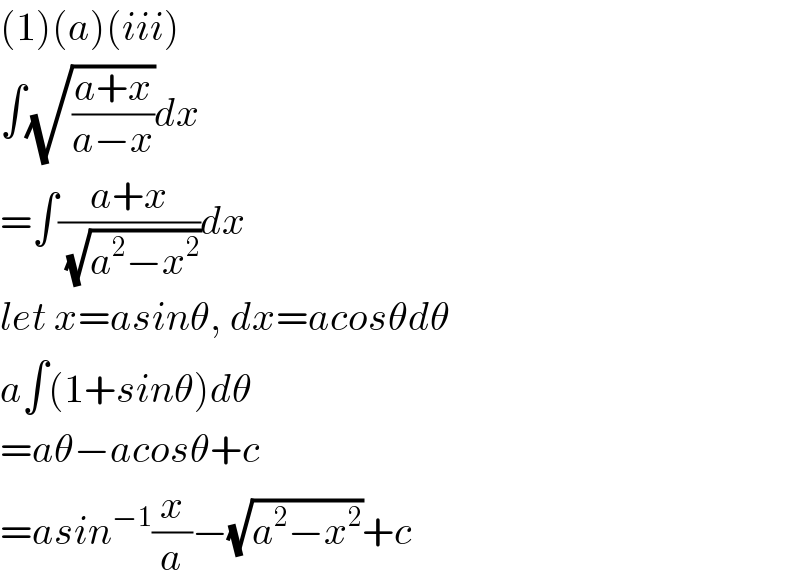
$$\left(\mathrm{1}\right)\left({a}\right)\left({iii}\right) \\ $$$$\int\sqrt{\frac{{a}+{x}}{{a}−{x}}}{dx} \\ $$$$=\int\frac{{a}+{x}}{\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{dx} \\ $$$${let}\:{x}={asin}\theta,\:{dx}={acos}\theta{d}\theta \\ $$$${a}\int\left(\mathrm{1}+{sin}\theta\right){d}\theta \\ $$$$={a}\theta−{acos}\theta+{c} \\ $$$$={asin}^{−\mathrm{1}} \frac{{x}}{{a}}−\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }+{c} \\ $$
Commented by Tony Lin last updated on 07/Jun/20
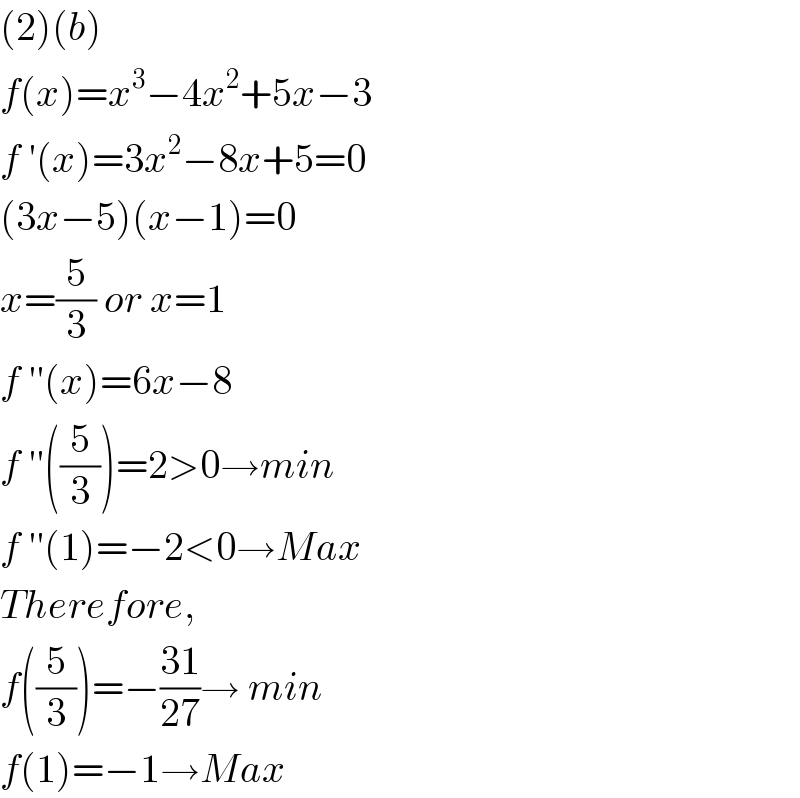
$$\left(\mathrm{2}\right)\left({b}\right) \\ $$$${f}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{3} \\ $$$${f}\:'\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{5}=\mathrm{0} \\ $$$$\left(\mathrm{3}{x}−\mathrm{5}\right)\left({x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\frac{\mathrm{5}}{\mathrm{3}}\:{or}\:{x}=\mathrm{1} \\ $$$${f}\:''\left({x}\right)=\mathrm{6}{x}−\mathrm{8} \\ $$$${f}\:''\left(\frac{\mathrm{5}}{\mathrm{3}}\right)=\mathrm{2}>\mathrm{0}\rightarrow{min} \\ $$$${f}\:''\left(\mathrm{1}\right)=−\mathrm{2}<\mathrm{0}\rightarrow{Max} \\ $$$${Therefore}, \\ $$$${f}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)=−\frac{\mathrm{31}}{\mathrm{27}}\rightarrow\:{min} \\ $$$${f}\left(\mathrm{1}\right)=−\mathrm{1}\rightarrow{Max} \\ $$
Commented by Tony Lin last updated on 07/Jun/20
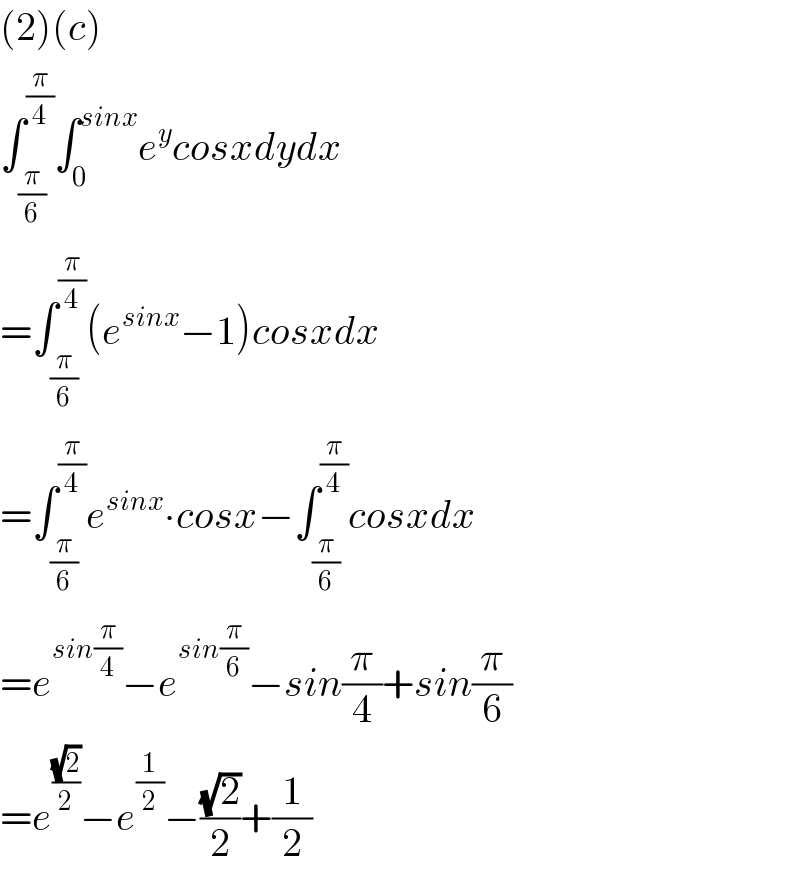
$$\left(\mathrm{2}\right)\left({c}\right) \\ $$$$\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{{sinx}} {e}^{{y}} {cosxdydx} \\ $$$$=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} \left({e}^{{sinx}} −\mathrm{1}\right){cosxdx} \\ $$$$=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} {e}^{{sinx}} \centerdot{cosx}−\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{4}}} {cosxdx} \\ $$$$={e}^{{sin}\frac{\pi}{\mathrm{4}}} −{e}^{{sin}\frac{\pi}{\mathrm{6}}} −{sin}\frac{\pi}{\mathrm{4}}+{sin}\frac{\pi}{\mathrm{6}} \\ $$$$={e}^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} −{e}^{\frac{\mathrm{1}}{\mathrm{2}}} −\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Tony Lin last updated on 07/Jun/20
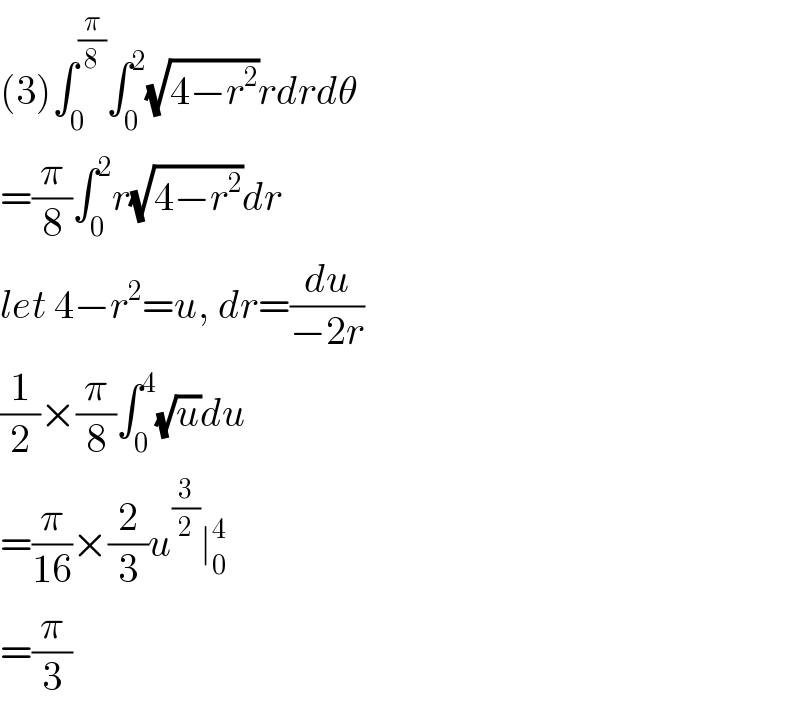
$$\left(\mathrm{3}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} \int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\mathrm{4}−{r}^{\mathrm{2}} }{rdrd}\theta \\ $$$$=\frac{\pi}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{2}} {r}\sqrt{\mathrm{4}−{r}^{\mathrm{2}} }{dr} \\ $$$${let}\:\mathrm{4}−{r}^{\mathrm{2}} ={u},\:{dr}=\frac{{du}}{−\mathrm{2}{r}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{4}} \sqrt{{u}}{du} \\ $$$$=\frac{\pi}{\mathrm{16}}×\frac{\mathrm{2}}{\mathrm{3}}{u}^{\frac{\mathrm{3}}{\mathrm{2}}} \mid_{\mathrm{0}} ^{\mathrm{4}} \\ $$$$=\frac{\pi}{\mathrm{3}} \\ $$
Commented by Tony Lin last updated on 07/Jun/20

$${All}\:{are}\:{done}! \\ $$
Commented by Riad last updated on 07/Jun/20
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}.\mathrm{love}\:\mathrm{you} \\ $$
Answered by mathmax by abdo last updated on 07/Jun/20
![3) I =∫∫_D (√(4−r^2 ))rdrdθ =∫_0 ^2 r(√(4−r^2 ))dr ∫_0 ^(π/8) dθ =(π/8) ∫_0 ^2 r(√(4−r^2 ))dr =(π/8) ∫_0 ^2 r(4−r^2 )^(1/2) dr =(π/8)[−(1/3)(4−r^2 )^(3/2) ]_0 ^2 =−(π/(24)){−4^(3/2) } =(π/(24))×8 =(π/3)](Q97406.png)
$$\left.\mathrm{3}\right)\:\mathrm{I}\:=\int\int_{\mathrm{D}} \sqrt{\mathrm{4}−\mathrm{r}^{\mathrm{2}} }\mathrm{rdrd}\theta\:\:=\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{r}\sqrt{\mathrm{4}−\mathrm{r}^{\mathrm{2}} }\mathrm{dr}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} \:\mathrm{d}\theta \\ $$$$=\frac{\pi}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{r}\sqrt{\mathrm{4}−\mathrm{r}^{\mathrm{2}} }\mathrm{dr}\:=\frac{\pi}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{r}\left(\mathrm{4}−\mathrm{r}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{dr}\:=\frac{\pi}{\mathrm{8}}\left[−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{4}−\mathrm{r}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=−\frac{\pi}{\mathrm{24}}\left\{−\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} \right\}\:=\frac{\pi}{\mathrm{24}}×\mathrm{8}\:=\frac{\pi}{\mathrm{3}} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 07/Jun/20
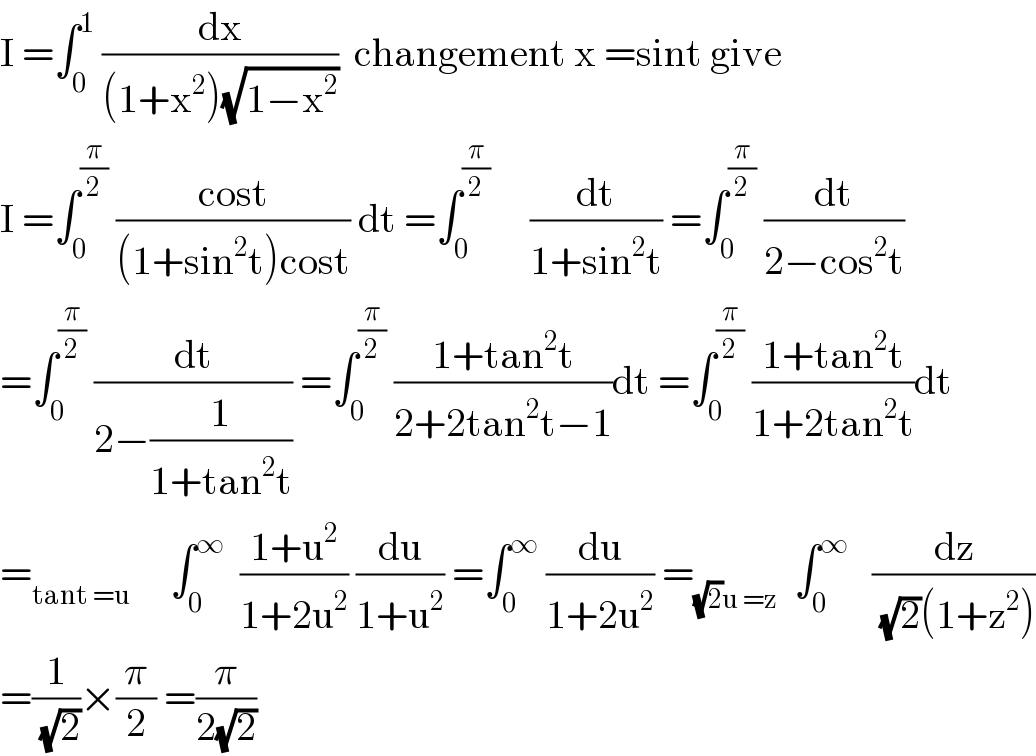
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{sint}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{cost}}{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \mathrm{t}\right)\mathrm{cost}}\:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \mathrm{t}}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dt}}{\mathrm{2}−\mathrm{cos}^{\mathrm{2}} \mathrm{t}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dt}}{\mathrm{2}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}}}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}}{\mathrm{2}+\mathrm{2tan}^{\mathrm{2}} \mathrm{t}−\mathrm{1}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}}{\mathrm{1}+\mathrm{2tan}^{\mathrm{2}} \mathrm{t}}\mathrm{dt} \\ $$$$=_{\mathrm{tant}\:=\mathrm{u}} \:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2u}^{\mathrm{2}} }\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{2u}^{\mathrm{2}} }\:=_{\sqrt{\mathrm{2}}\mathrm{u}\:=\mathrm{z}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{dz}}{\sqrt{\mathrm{2}}\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Answered by mathmax by abdo last updated on 07/Jun/20
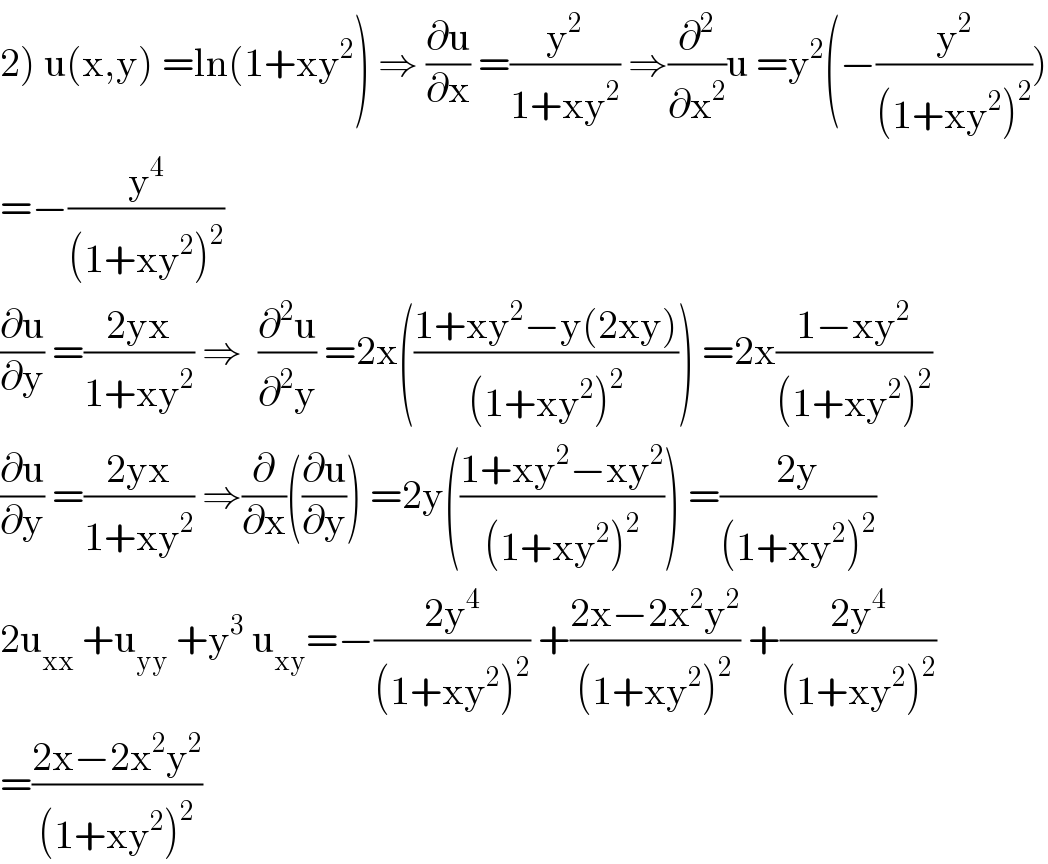
$$\left.\mathrm{2}\right)\:\mathrm{u}\left(\mathrm{x},\mathrm{y}\right)\:=\mathrm{ln}\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)\:\Rightarrow\:\frac{\partial\mathrm{u}}{\partial\mathrm{x}}\:=\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{xy}^{\mathrm{2}} }\:\Rightarrow\frac{\partial^{\mathrm{2}} }{\partial\mathrm{x}^{\mathrm{2}} }\mathrm{u}\:=\mathrm{y}^{\mathrm{2}} \left(−\frac{\mathrm{y}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{2}} }\right) \\ $$$$=−\frac{\mathrm{y}^{\mathrm{4}} }{\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\frac{\partial\mathrm{u}}{\partial\mathrm{y}}\:=\frac{\mathrm{2yx}}{\mathrm{1}+\mathrm{xy}^{\mathrm{2}} }\:\Rightarrow\:\:\frac{\partial^{\mathrm{2}} \mathrm{u}}{\partial^{\mathrm{2}} \mathrm{y}}\:=\mathrm{2x}\left(\frac{\mathrm{1}+\mathrm{xy}^{\mathrm{2}} −\mathrm{y}\left(\mathrm{2xy}\right)}{\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{2}} }\right)\:=\mathrm{2x}\frac{\mathrm{1}−\mathrm{xy}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\frac{\partial\mathrm{u}}{\partial\mathrm{y}}\:=\frac{\mathrm{2yx}}{\mathrm{1}+\mathrm{xy}^{\mathrm{2}} }\:\Rightarrow\frac{\partial}{\partial\mathrm{x}}\left(\frac{\partial\mathrm{u}}{\partial\mathrm{y}}\right)\:=\mathrm{2y}\left(\frac{\mathrm{1}+\mathrm{xy}^{\mathrm{2}} −\mathrm{xy}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{2}} }\right)\:=\frac{\mathrm{2y}}{\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{2u}_{\mathrm{xx}} \:+\mathrm{u}_{\mathrm{yy}} \:+\mathrm{y}^{\mathrm{3}} \:\mathrm{u}_{\mathrm{xy}} =−\frac{\mathrm{2y}^{\mathrm{4}} }{\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{2}} }\:+\frac{\mathrm{2x}−\mathrm{2x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{2}} }\:+\frac{\mathrm{2y}^{\mathrm{4}} }{\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2x}−\mathrm{2x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{xy}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$
