
Question Number 97157 by mhmd last updated on 06/Jun/20
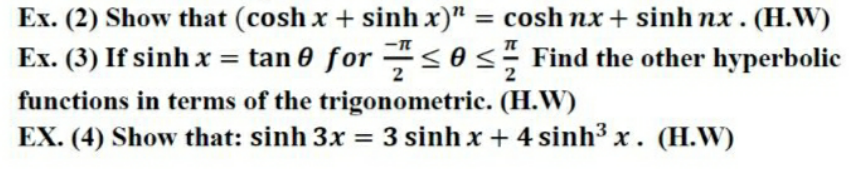
Commented by mhmd last updated on 06/Jun/20
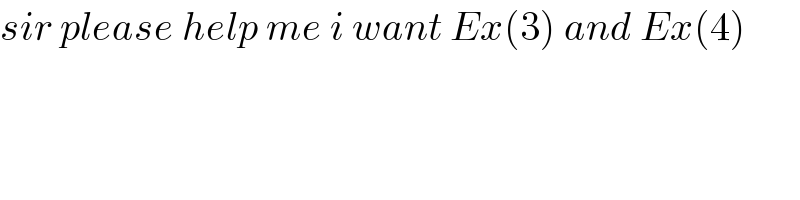
$${sir}\:{please}\:{help}\:{me}\:{i}\:{want}\:{Ex}\left(\mathrm{3}\right)\:{and}\:{Ex}\left(\mathrm{4}\right) \\ $$
Answered by Sourav mridha last updated on 06/Jun/20
![Ex(2).coshx=((e^x +e^(−x) )/2) sinhx=((e^x −e^(−x) )/2) (coshx+sinhx)^n =e^(nx) =[((e^(nx) +e^(−nx) )/2)+((e^(nx) −e^(−nx) )/2)] = cosh(nx)+sinh(nx)](Q97161.png)
$$\boldsymbol{{E}}\mathrm{x}\left(\mathrm{2}\right).\boldsymbol{{coshx}}=\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} +\boldsymbol{{e}}^{−\boldsymbol{{x}}} }{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{sinhx}}=\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} −\boldsymbol{{e}}^{−\boldsymbol{{x}}} }{\mathrm{2}} \\ $$$$\left(\boldsymbol{{coshx}}+\boldsymbol{{sinhx}}\right)^{\boldsymbol{{n}}} =\boldsymbol{{e}}^{\boldsymbol{{nx}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left[\frac{\boldsymbol{{e}}^{\boldsymbol{{nx}}} +\boldsymbol{{e}}^{−\boldsymbol{{nx}}} }{\mathrm{2}}+\frac{\boldsymbol{{e}}^{\boldsymbol{{nx}}} −\boldsymbol{{e}}^{−\boldsymbol{{nx}}} }{\mathrm{2}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\boldsymbol{{cosh}}\left(\boldsymbol{{nx}}\right)+\boldsymbol{{sinh}}\left(\boldsymbol{{nx}}\right) \\ $$
Commented by mhmd last updated on 06/Jun/20
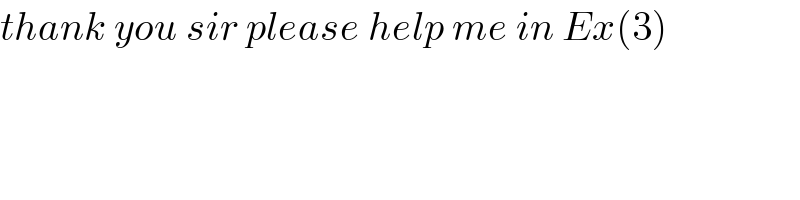
$${thank}\:{you}\:{sir}\:{please}\:{help}\:{me}\:{in}\:{Ex}\left(\mathrm{3}\right) \\ $$
Answered by Sourav mridha last updated on 06/Jun/20
![Ex(4)sinh(3x)=((e^(3x) −e^(−3x) )/2) =(1/2)[(e^x −e^(−x) )^3 +3e^x .e^(−x) (e^x −e^(−x) )] =3[((e^x −e^(−x) )/2)]+(2^3 /2)[((e^x −e^(−x) )/2)]^3 =3sinh(x)+4sinh^3 (x).](Q97163.png)
$$\boldsymbol{{Ex}}\left(\mathrm{4}\right)\boldsymbol{{sinh}}\left(\mathrm{3}\boldsymbol{{x}}\right)=\frac{\boldsymbol{{e}}^{\mathrm{3}\boldsymbol{{x}}} −\boldsymbol{{e}}^{−\mathrm{3}\boldsymbol{{x}}} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\boldsymbol{{e}}^{\boldsymbol{{x}}} −\boldsymbol{{e}}^{−\boldsymbol{{x}}} \right)^{\mathrm{3}} +\mathrm{3}\boldsymbol{{e}}^{\boldsymbol{{x}}} .\boldsymbol{{e}}^{−\boldsymbol{{x}}} \left(\boldsymbol{{e}}^{\boldsymbol{{x}}} −\boldsymbol{{e}}^{−\boldsymbol{{x}}} \right)\right] \\ $$$$=\mathrm{3}\left[\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} −\boldsymbol{{e}}^{−\boldsymbol{{x}}} }{\mathrm{2}}\right]+\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{2}}\left[\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} −\boldsymbol{{e}}^{−\boldsymbol{{x}}} }{\mathrm{2}}\right]^{\mathrm{3}} \\ $$$$=\mathrm{3}\boldsymbol{{sinh}}\left(\boldsymbol{{x}}\right)+\mathrm{4}\boldsymbol{{sinh}}^{\mathrm{3}} \left(\boldsymbol{{x}}\right). \\ $$
Answered by mathmax by abdo last updated on 06/Jun/20
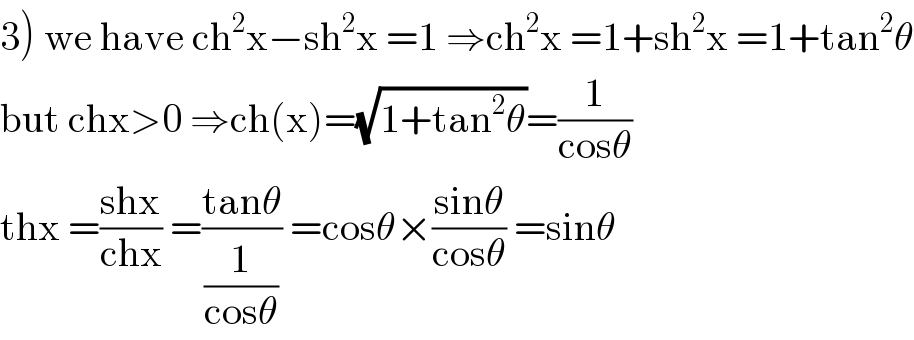
$$\left.\mathrm{3}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{ch}^{\mathrm{2}} \mathrm{x}−\mathrm{sh}^{\mathrm{2}} \mathrm{x}\:=\mathrm{1}\:\Rightarrow\mathrm{ch}^{\mathrm{2}} \mathrm{x}\:=\mathrm{1}+\mathrm{sh}^{\mathrm{2}} \mathrm{x}\:=\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta \\ $$$$\mathrm{but}\:\mathrm{chx}>\mathrm{0}\:\Rightarrow\mathrm{ch}\left(\mathrm{x}\right)=\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}=\frac{\mathrm{1}}{\mathrm{cos}\theta} \\ $$$$\mathrm{thx}\:=\frac{\mathrm{shx}}{\mathrm{chx}}\:=\frac{\mathrm{tan}\theta}{\frac{\mathrm{1}}{\mathrm{cos}\theta}}\:=\mathrm{cos}\theta×\frac{\mathrm{sin}\theta}{\mathrm{cos}\theta}\:=\mathrm{sin}\theta \\ $$
