
Question Number 97143 by Ar Brandon last updated on 06/Jun/20
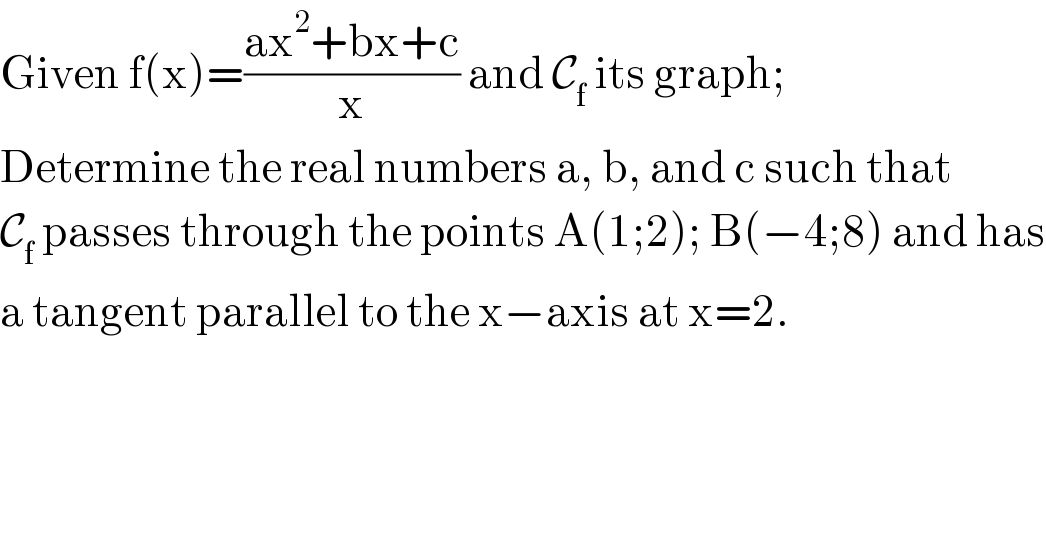
$$\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}}{\mathrm{x}}\:\mathrm{and}\:\mathcal{C}_{\mathrm{f}} \:\mathrm{its}\:\mathrm{graph}; \\ $$$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{a},\:\mathrm{b},\:\mathrm{and}\:\mathrm{c}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathcal{C}_{\mathrm{f}} \:\mathrm{passes}\:\mathrm{through}\:\mathrm{the}\:\mathrm{points}\:\mathrm{A}\left(\mathrm{1};\mathrm{2}\right);\:\mathrm{B}\left(−\mathrm{4};\mathrm{8}\right)\:\mathrm{and}\:\mathrm{has} \\ $$$$\mathrm{a}\:\mathrm{tangent}\:\mathrm{parallel}\:\mathrm{to}\:\mathrm{the}\:\mathrm{x}−\mathrm{axis}\:\mathrm{at}\:\mathrm{x}=\mathrm{2}. \\ $$
Answered by MJS last updated on 06/Jun/20

$$\mathrm{just}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{linear}\:\mathrm{system} \\ $$$$\begin{cases}{{f}\left(\mathrm{1}\right)=\mathrm{2}}\\{{f}\left(−\mathrm{4}\right)=\mathrm{8}}\\{{f}'\left(\mathrm{2}\right)=\mathrm{0}}\end{cases} \\ $$$$\mathrm{for}\:{a},\:{b},\:{c} \\ $$$$\Rightarrow \\ $$$${a}=−\frac{\mathrm{3}}{\mathrm{5}};\:{b}=\mathrm{5};\:{c}=−\frac{\mathrm{12}}{\mathrm{5}} \\ $$
