
Question Number 97142 by mhmd last updated on 06/Jun/20
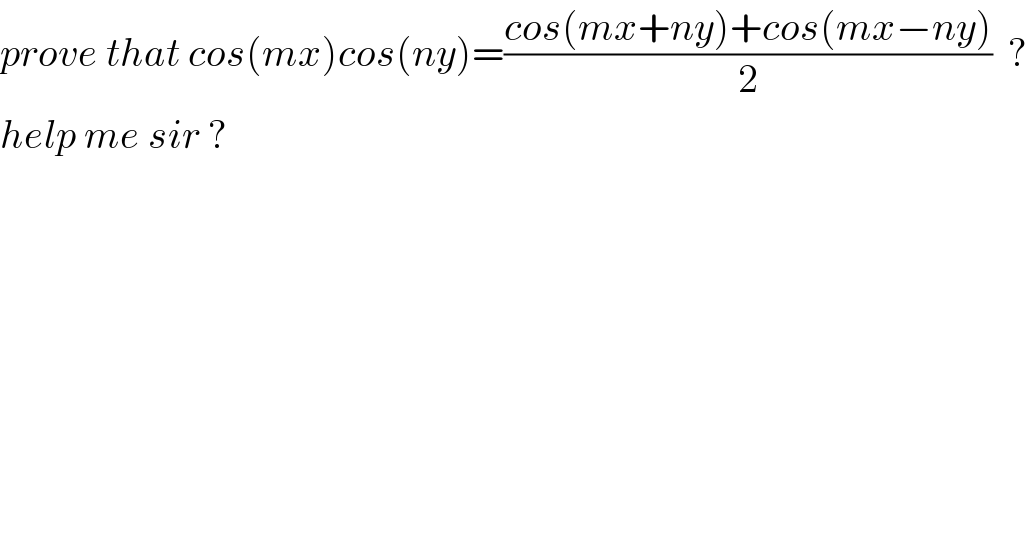
$${prove}\:{that}\:{cos}\left({mx}\right){cos}\left({ny}\right)=\frac{{cos}\left({mx}+{ny}\right)+{cos}\left({mx}−{ny}\right)}{\mathrm{2}}\:\:? \\ $$$${help}\:{me}\:{sir}\:? \\ $$
Commented by mr W last updated on 06/Jun/20

$${just}\:{apply}\:{the}\:{formulae}\:{for} \\ $$$$\mathrm{cos}\:\left({a}+{b}\right)\:{and}\:\mathrm{cos}\:\left({a}−{b}\right). \\ $$
Commented by mhmd last updated on 06/Jun/20
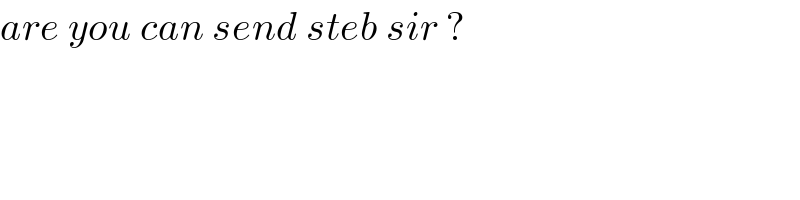
$${are}\:{you}\:{can}\:{send}\:{steb}\:{sir}\:? \\ $$
Commented by mr W last updated on 06/Jun/20

$${i}\:{can},\:{but}\:{i}\:{don}'{t}\:{want}\:{to}\:{do}! \\ $$$${if}\:{you}\:{don}'{t}\:{know}\:{the}\:{formulae}\:{for}\: \\ $$$$\mathrm{cos}\:\left({a}+{b}\right)\:{and}\:\mathrm{cos}\:\left({a}−{b}\right)\:{or}\:{how}\:{to} \\ $$$${apply}\:{them},\:{it}\:{means}\:{you}\:{have}\:{not} \\ $$$${learnt}\:{trigonometry}\:{yet},\:{then} \\ $$$${you}\:{won}'{t}\:{be}\:{able}\:{to}\:{understand} \\ $$$${the}\:{answer}\:{even}\:{if}\:{it}\:{is} \\ $$$${step}\:{by}\:{step}.\:{in}\:{this}\:{case}\:{it}\:{has} \\ $$$${totally}\:{just}\:{one}\:{step}. \\ $$
Answered by mathmax by abdo last updated on 06/Jun/20
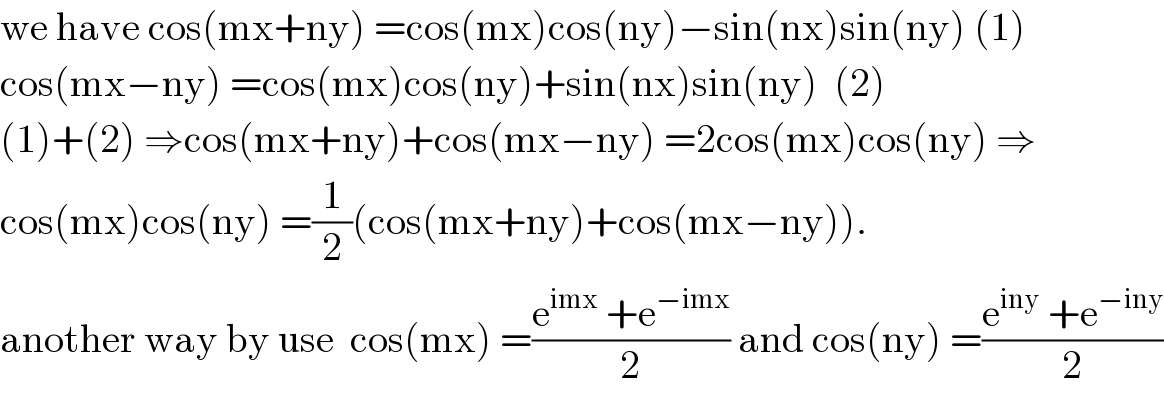
$$\mathrm{we}\:\mathrm{have}\:\mathrm{cos}\left(\mathrm{mx}+\mathrm{ny}\right)\:=\mathrm{cos}\left(\mathrm{mx}\right)\mathrm{cos}\left(\mathrm{ny}\right)−\mathrm{sin}\left(\mathrm{nx}\right)\mathrm{sin}\left(\mathrm{ny}\right)\:\left(\mathrm{1}\right) \\ $$$$\mathrm{cos}\left(\mathrm{mx}−\mathrm{ny}\right)\:=\mathrm{cos}\left(\mathrm{mx}\right)\mathrm{cos}\left(\mathrm{ny}\right)+\mathrm{sin}\left(\mathrm{nx}\right)\mathrm{sin}\left(\mathrm{ny}\right)\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\:\Rightarrow\mathrm{cos}\left(\mathrm{mx}+\mathrm{ny}\right)+\mathrm{cos}\left(\mathrm{mx}−\mathrm{ny}\right)\:=\mathrm{2cos}\left(\mathrm{mx}\right)\mathrm{cos}\left(\mathrm{ny}\right)\:\Rightarrow \\ $$$$\mathrm{cos}\left(\mathrm{mx}\right)\mathrm{cos}\left(\mathrm{ny}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\left(\mathrm{mx}+\mathrm{ny}\right)+\mathrm{cos}\left(\mathrm{mx}−\mathrm{ny}\right)\right). \\ $$$$\mathrm{another}\:\mathrm{way}\:\mathrm{by}\:\mathrm{use}\:\:\mathrm{cos}\left(\mathrm{mx}\right)\:=\frac{\mathrm{e}^{\mathrm{imx}} \:+\mathrm{e}^{−\mathrm{imx}} }{\mathrm{2}}\:\mathrm{and}\:\mathrm{cos}\left(\mathrm{ny}\right)\:=\frac{\mathrm{e}^{\mathrm{iny}} \:+\mathrm{e}^{−\mathrm{iny}} }{\mathrm{2}} \\ $$
Answered by 1549442205 last updated on 07/Jun/20

$$\mathrm{The}\:\mathrm{formulas}\:\mathrm{to}\:\mathrm{transform}\:\mathrm{in}\:\mathrm{trigonometry}\:\mathrm{as}: \\ $$$$\left.\boldsymbol{\mathrm{i}}\right)\:\boldsymbol{\mathrm{cos}\varphi}+\boldsymbol{\mathrm{cos}\psi}=\mathrm{2}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\varphi}+\boldsymbol{\psi}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\varphi}−\boldsymbol{\psi}}{\mathrm{2}} \\ $$$$\left.\boldsymbol{\mathrm{ii}}\right)\:\boldsymbol{\mathrm{cos}\varphi}−\boldsymbol{\mathrm{cos}\psi}=−\mathrm{2}\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\varphi}+\boldsymbol{\psi}}{\mathrm{2}}\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\varphi}−\boldsymbol{\psi}}{\mathrm{2}} \\ $$$$\left.\boldsymbol{\mathrm{iii}}\right)\boldsymbol{\mathrm{sin}\varphi}+\boldsymbol{\mathrm{sin}\psi}=\mathrm{2}\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\varphi}+\boldsymbol{\psi}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\varphi}−\boldsymbol{\psi}}{\mathrm{2}} \\ $$$$\left.\boldsymbol{\mathrm{iv}}\right)\boldsymbol{\mathrm{sin}\varphi}−\boldsymbol{\mathrm{sin}\psi}=\mathrm{2}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\varphi}+\boldsymbol{\psi}}{\mathrm{2}}\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\varphi}−\boldsymbol{\psi}}{\mathrm{2}} \\ $$
