Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 96244 by Don08q last updated on 31/May/20

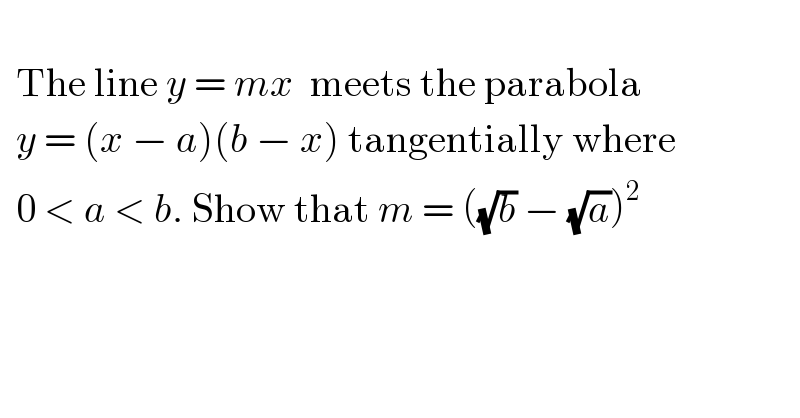
The line y = mx meets the parabola y = (x − a)(b − x) tangentially where 0 < a < b. Show that m = ((√b) − (√a))^2

$$ \\ $$ $$\:\:\mathrm{The}\:\mathrm{line}\:{y}\:=\:{mx}\:\:\mathrm{meets}\:\mathrm{the}\:\mathrm{parabola} \\ $$ $$\:\:{y}\:=\:\left({x}\:−\:{a}\right)\left({b}\:−\:{x}\right)\:\mathrm{tangentially}\:\mathrm{where} \\ $$ $$\:\:\mathrm{0}\:<\:{a}\:<\:{b}.\:\mathrm{Show}\:\mathrm{that}\:{m}\:=\:\left(\sqrt{{b}}\:−\:\sqrt{{a}}\right)^{\mathrm{2}} \\ $$ $$ \\ $$

Commented bybobhans last updated on 31/May/20

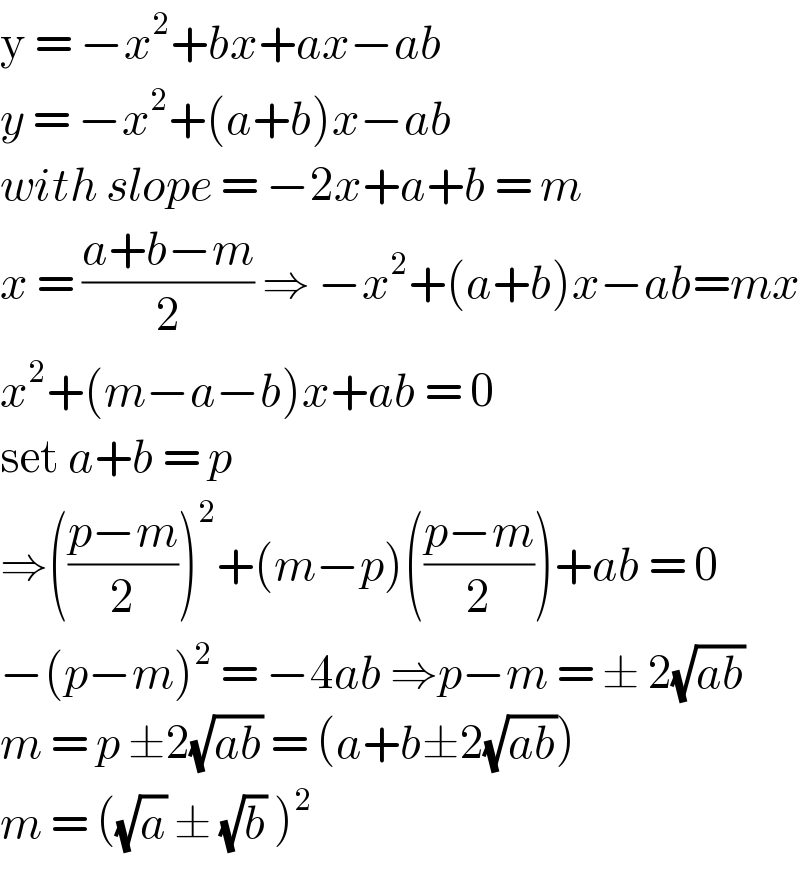
y = −x^2 +bx+ax−ab y = −x^2 +(a+b)x−ab with slope = −2x+a+b = m x = ((a+b−m)/2) ⇒ −x^2 +(a+b)x−ab=mx x^2 +(m−a−b)x+ab = 0 set a+b = p ⇒(((p−m)/2))^2 +(m−p)(((p−m)/2))+ab = 0 −(p−m)^2 = −4ab ⇒p−m = ± 2(√(ab)) m = p ±2(√(ab)) = (a+b±2(√(ab))) m = ((√a) ± (√b) )^2

$$\mathrm{y}\:=\:−{x}^{\mathrm{2}} +{bx}+{ax}−{ab}\: \\ $$ $${y}\:=\:−{x}^{\mathrm{2}} +\left({a}+{b}\right){x}−{ab}\: \\ $$ $${with}\:{slope}\:=\:−\mathrm{2}{x}+{a}+{b}\:=\:{m}\: \\ $$ $${x}\:=\:\frac{{a}+{b}−{m}}{\mathrm{2}}\:\Rightarrow\:−{x}^{\mathrm{2}} +\left({a}+{b}\right){x}−{ab}={mx} \\ $$ $${x}^{\mathrm{2}} +\left({m}−{a}−{b}\right){x}+{ab}\:=\:\mathrm{0} \\ $$ $$\mathrm{set}\:{a}+{b}\:=\:{p} \\ $$ $$\Rightarrow\left(\frac{{p}−{m}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({m}−{p}\right)\left(\frac{{p}−{m}}{\mathrm{2}}\right)+{ab}\:=\:\mathrm{0} \\ $$ $$−\left({p}−{m}\right)^{\mathrm{2}} \:=\:−\mathrm{4}{ab}\:\Rightarrow{p}−{m}\:=\:\pm\:\mathrm{2}\sqrt{{ab}} \\ $$ $${m}\:=\:{p}\:\pm\mathrm{2}\sqrt{{ab}}\:=\:\left({a}+{b}\pm\mathrm{2}\sqrt{{ab}}\right) \\ $$ $${m}\:=\:\left(\sqrt{{a}}\:\pm\:\sqrt{{b}}\:\right)^{\mathrm{2}} \: \\ $$

Commented byDon08q last updated on 31/May/20

Thank you Sir.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}. \\ $$

Answered by Smail last updated on 31/May/20

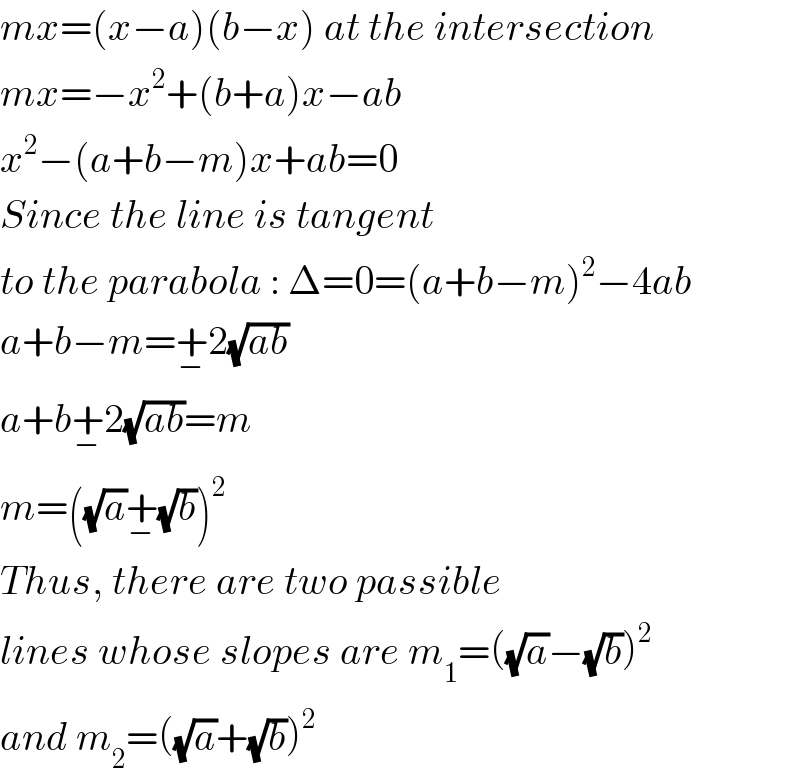
mx=(x−a)(b−x) at the intersection mx=−x^2 +(b+a)x−ab x^2 −(a+b−m)x+ab=0 Since the line is tangent to the parabola : Δ=0=(a+b−m)^2 −4ab a+b−m=+_− 2(√(ab)) a+b+_− 2(√(ab))=m m=((√a)+_− (√b))^2 Thus, there are two passible lines whose slopes are m_1 =((√a)−(√b))^2 and m_2 =((√a)+(√b))^2

$${mx}=\left({x}−{a}\right)\left({b}−{x}\right)\:{at}\:{the}\:{intersection} \\ $$ $${mx}=−{x}^{\mathrm{2}} +\left({b}+{a}\right){x}−{ab}\: \\ $$ $${x}^{\mathrm{2}} −\left({a}+{b}−{m}\right){x}+{ab}=\mathrm{0} \\ $$ $${Since}\:{the}\:{line}\:{is}\:{tangent}\: \\ $$ $${to}\:{the}\:{parabola}\::\:\Delta=\mathrm{0}=\left({a}+{b}−{m}\right)^{\mathrm{2}} −\mathrm{4}{ab} \\ $$ $${a}+{b}−{m}=\underset{−} {+}\mathrm{2}\sqrt{{ab}} \\ $$ $${a}+{b}\underset{−} {+}\mathrm{2}\sqrt{{ab}}={m} \\ $$ $${m}=\left(\sqrt{{a}}\underset{−} {+}\sqrt{{b}}\right)^{\mathrm{2}} \\ $$ $${Thus},\:{there}\:{are}\:{two}\:{passible} \\ $$ $${lines}\:{whose}\:{slopes}\:{are}\:{m}_{\mathrm{1}} =\left(\sqrt{{a}}−\sqrt{{b}}\right)^{\mathrm{2}} \\ $$ $${and}\:{m}_{\mathrm{2}} =\left(\sqrt{{a}}+\sqrt{{b}}\right)^{\mathrm{2}} \\ $$

Commented byDon08q last updated on 31/May/20

Thank you Sir.

$$\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com