Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 9517 by Joel575 last updated on 12/Dec/16

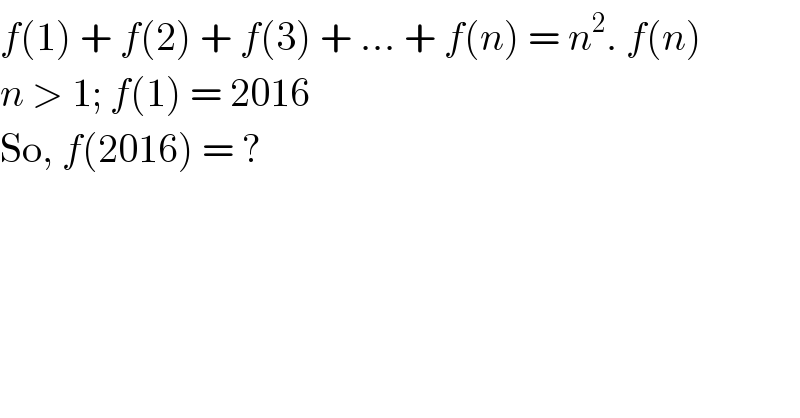
f(1) + f(2) + f(3) + ... + f(n) = n^2 . f(n) n > 1; f(1) = 2016 So, f(2016) = ?

$${f}\left(\mathrm{1}\right)\:+\:{f}\left(\mathrm{2}\right)\:+\:{f}\left(\mathrm{3}\right)\:+\:...\:+\:{f}\left({n}\right)\:=\:{n}^{\mathrm{2}} .\:{f}\left({n}\right) \\ $$ $${n}\:>\:\mathrm{1};\:{f}\left(\mathrm{1}\right)\:=\:\mathrm{2016} \\ $$ $$\mathrm{So},\:{f}\left(\mathrm{2016}\right)\:=\:? \\ $$

Commented bysou1618 last updated on 12/Dec/16

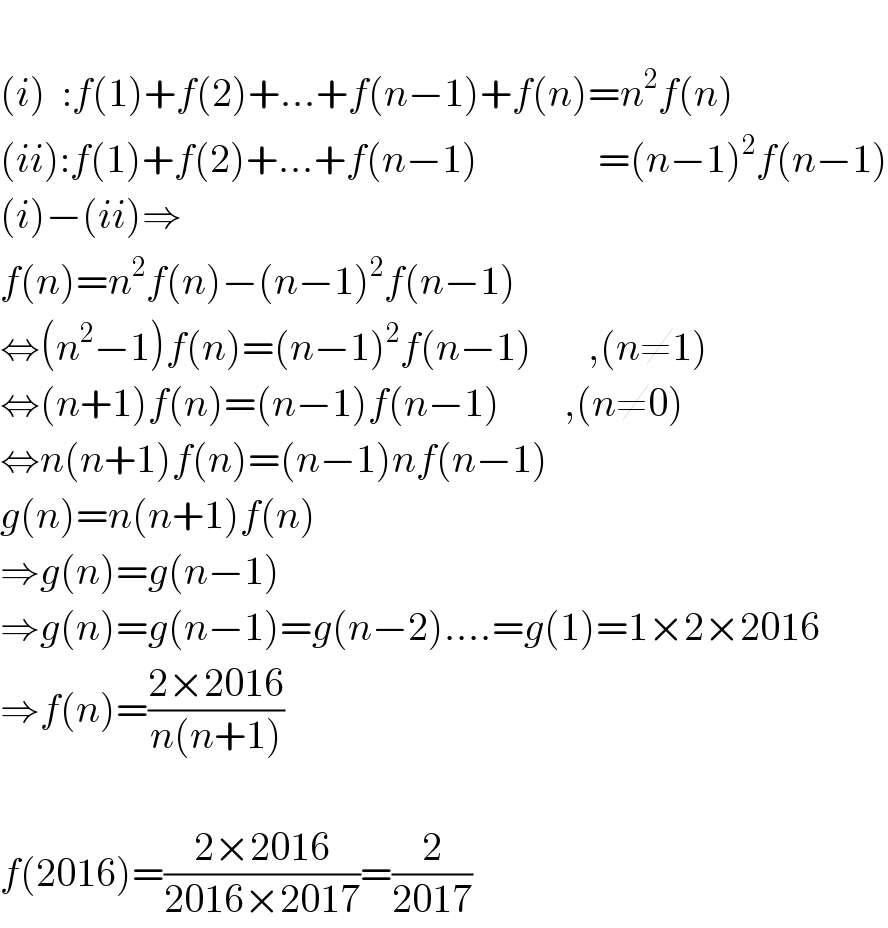
(i) :f(1)+f(2)+...+f(n−1)+f(n)=n^2 f(n) (ii):f(1)+f(2)+...+f(n−1) =(n−1)^2 f(n−1) (i)−(ii)⇒ f(n)=n^2 f(n)−(n−1)^2 f(n−1) ⇔(n^2 −1)f(n)=(n−1)^2 f(n−1) ,(n≠1) ⇔(n+1)f(n)=(n−1)f(n−1) ,(n≠0) ⇔n(n+1)f(n)=(n−1)nf(n−1) g(n)=n(n+1)f(n) ⇒g(n)=g(n−1) ⇒g(n)=g(n−1)=g(n−2)....=g(1)=1×2×2016 ⇒f(n)=((2×2016)/(n(n+1))) f(2016)=((2×2016)/(2016×2017))=(2/(2017))

$$ \\ $$ $$\left({i}\right)\:\::{f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)+...+{f}\left({n}−\mathrm{1}\right)+{f}\left({n}\right)={n}^{\mathrm{2}} {f}\left({n}\right) \\ $$ $$\left({ii}\right):{f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)+...+{f}\left({n}−\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({n}−\mathrm{1}\right)^{\mathrm{2}} {f}\left({n}−\mathrm{1}\right) \\ $$ $$\left({i}\right)−\left({ii}\right)\Rightarrow \\ $$ $${f}\left({n}\right)={n}^{\mathrm{2}} {f}\left({n}\right)−\left({n}−\mathrm{1}\right)^{\mathrm{2}} {f}\left({n}−\mathrm{1}\right) \\ $$ $$\Leftrightarrow\left({n}^{\mathrm{2}} −\mathrm{1}\right){f}\left({n}\right)=\left({n}−\mathrm{1}\right)^{\mathrm{2}} {f}\left({n}−\mathrm{1}\right)\:\:\:\:\:\:\:,\left({n}\neq\mathrm{1}\right) \\ $$ $$\Leftrightarrow\left({n}+\mathrm{1}\right){f}\left({n}\right)=\left({n}−\mathrm{1}\right){f}\left({n}−\mathrm{1}\right)\:\:\:\:\:\:\:\:,\left({n}\neq\mathrm{0}\right) \\ $$ $$\Leftrightarrow{n}\left({n}+\mathrm{1}\right){f}\left({n}\right)=\left({n}−\mathrm{1}\right){nf}\left({n}−\mathrm{1}\right) \\ $$ $${g}\left({n}\right)={n}\left({n}+\mathrm{1}\right){f}\left({n}\right) \\ $$ $$\Rightarrow{g}\left({n}\right)={g}\left({n}−\mathrm{1}\right) \\ $$ $$\Rightarrow{g}\left({n}\right)={g}\left({n}−\mathrm{1}\right)={g}\left({n}−\mathrm{2}\right)....={g}\left(\mathrm{1}\right)=\mathrm{1}×\mathrm{2}×\mathrm{2016} \\ $$ $$\Rightarrow{f}\left({n}\right)=\frac{\mathrm{2}×\mathrm{2016}}{{n}\left({n}+\mathrm{1}\right)} \\ $$ $$ \\ $$ $${f}\left(\mathrm{2016}\right)=\frac{\mathrm{2}×\mathrm{2016}}{\mathrm{2016}×\mathrm{2017}}=\frac{\mathrm{2}}{\mathrm{2017}} \\ $$

Commented byJoel575 last updated on 12/Dec/16

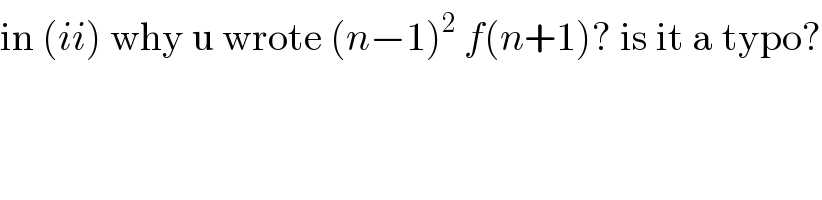
in (ii) why u wrote (n−1)^2 f(n+1)? is it a typo?

$$\mathrm{in}\:\left({ii}\right)\:\mathrm{why}\:\mathrm{u}\:\mathrm{wrote}\:\left({n}−\mathrm{1}\right)^{\mathrm{2}} \:{f}\left({n}+\mathrm{1}\right)?\:\mathrm{is}\:\mathrm{it}\:\mathrm{a}\:\mathrm{typo}? \\ $$

Commented bysou1618 last updated on 12/Dec/16

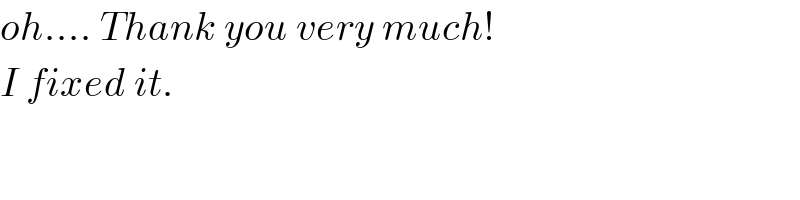
oh.... Thank you very much! I fixed it.

$${oh}....\:{Thank}\:{you}\:{very}\:{much}! \\ $$ $${I}\:{fixed}\:{it}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com