
Question Number 95093 by I want to learn more last updated on 22/May/20
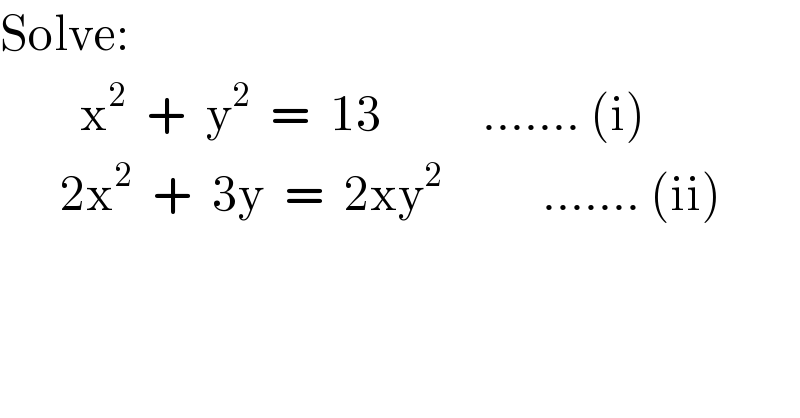
$$\mathrm{Solve}: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \:\:+\:\:\mathrm{y}^{\mathrm{2}} \:\:=\:\:\mathrm{13}\:\:\:\:\:\:\:\:\:\:.......\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\mathrm{2x}^{\mathrm{2}} \:\:+\:\:\mathrm{3y}\:\:=\:\:\mathrm{2xy}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:.......\:\left(\mathrm{ii}\right) \\ $$
Answered by behi83417@gmail.com last updated on 23/May/20

$$\left(\mathrm{2}×\mathrm{i}−\mathrm{ii}\right)\Rightarrow\mathrm{2y}^{\mathrm{2}} −\mathrm{3y}=\mathrm{26}−\mathrm{2xy}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{26}+\mathrm{3y}−\mathrm{2y}^{\mathrm{2}} }{\mathrm{2y}^{\mathrm{2}} } \\ $$$$\Rightarrow\left(\frac{\mathrm{26}+\mathrm{3y}−\mathrm{2y}^{\mathrm{2}} }{\mathrm{2y}^{\mathrm{2}} }\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{13} \\ $$$$\left(\mathrm{26}+\mathrm{3y}−\mathrm{2y}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4y}^{\mathrm{6}} =\mathrm{52y}^{\mathrm{4}} \\ $$$$\mathrm{676}+\mathrm{9y}^{\mathrm{2}} +\mathrm{4y}^{\mathrm{4}} +\mathrm{156y}−\mathrm{104y}^{\mathrm{2}} −\mathrm{12y}^{\mathrm{3}} +\mathrm{4y}^{\mathrm{6}} =\mathrm{52y}^{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{4y}^{\mathrm{6}} −\mathrm{48y}^{\mathrm{4}} −\mathrm{12y}^{\mathrm{3}} −\mathrm{95y}^{\mathrm{2}} +\mathrm{156y}+\mathrm{676}=\mathrm{0} \\ $$$$\left(\mathrm{y}−\mathrm{2}\right)\left(\:\:\mathrm{p}\left(\mathrm{y}\right)\:\:\right)=\mathrm{0}\Rightarrow \\ $$$$\Rightarrow\mathrm{y}=\mathrm{2}\:\:,\pm\mathrm{3}.\mathrm{6},−\mathrm{1}.\mathrm{6} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{3},\pm\mathrm{0}.\mathrm{43},\mathrm{3}.\mathrm{14} \\ $$
Commented by I want to learn more last updated on 23/May/20

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
Answered by 1549442205 last updated on 23/May/20
![From (1)we have y^2 =13−x^2 ,putting into (ii) we get y=((−2x^3 −2x^2 +26x)/3).Squaring we get((4x^(6 ) +8x^5 +4x^4 +676x^2 −104x^4 −104x^3 )/9). Putting into (i)we get 4x^6 +8x^5 −100x^4 − 104x^3 +685x^2 −117=0.This equation has four real roots: x_1 =−0.4058529736 and 0.4337536916,x_3 =3 and Res x_4 =3.23939445877281 pectively,we get y_1 =−3.582636371 and y_2 =3.579365549,y_3 =2 and y_4 =1.583137246.Thus,our system of equations has four solutions: (x;y)∈{(x_1 ;y_1 );(x_2 ;y_2 );(x_3 ,y_3 );(x_4 ;y_4 )} [ (y/(x^2 +y^2 )) + (x/(x^2 +y^2 )) ] dx + [(y/(x^2 +y^2 ))−(x/(x^2 +y^2 )) ]dy=0](Q95109.png)
$$\mathrm{From}\:\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{have}\:\mathrm{y}^{\mathrm{2}} =\mathrm{13}−\mathrm{x}^{\mathrm{2}} ,\mathrm{putting}\:\mathrm{into} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{we}\:\mathrm{get}\:\:\mathrm{y}=\frac{−\mathrm{2x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} +\mathrm{26x}}{\mathrm{3}}.\mathrm{Squaring} \\ $$$$\mathrm{we}\:\mathrm{get}\frac{\mathrm{4x}^{\mathrm{6}\:} +\mathrm{8x}^{\mathrm{5}} +\mathrm{4x}^{\mathrm{4}} +\mathrm{676x}^{\mathrm{2}} −\mathrm{104x}^{\mathrm{4}} −\mathrm{104x}^{\mathrm{3}} }{\mathrm{9}}. \\ $$$$\mathrm{Putting}\:\mathrm{into}\:\left(\mathrm{i}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{4x}^{\mathrm{6}} +\mathrm{8x}^{\mathrm{5}} −\mathrm{100x}^{\mathrm{4}} − \\ $$$$\mathrm{104x}^{\mathrm{3}} +\mathrm{685x}^{\mathrm{2}} −\mathrm{117}=\mathrm{0}.\mathrm{This}\:\mathrm{equation}\:\:\mathrm{has}\:\:\mathrm{four}\:\mathrm{real}\:\mathrm{roots}: \\ $$$$\mathrm{x}_{\mathrm{1}} =−\mathrm{0}.\mathrm{4058529736}\:\mathrm{and}\:\mathrm{0}.\mathrm{4337536916},\mathrm{x}_{\mathrm{3}} =\mathrm{3}\:\mathrm{and}\:\mathrm{Res} \\ $$$$\mathrm{x}_{\mathrm{4}} =\mathrm{3}.\mathrm{23939445877281} \\ $$$$\mathrm{pectively},\mathrm{we}\:\mathrm{get}\:\mathrm{y}_{\mathrm{1}} =−\mathrm{3}.\mathrm{582636371}\:\mathrm{and} \\ $$$$\mathrm{y}_{\mathrm{2}} =\mathrm{3}.\mathrm{579365549},\mathrm{y}_{\mathrm{3}} =\mathrm{2}\:\mathrm{and}\:\mathrm{y}_{\mathrm{4}} =\mathrm{1}.\mathrm{583137246}.\mathrm{Thus},\mathrm{our}\:\mathrm{system}\:\mathrm{of} \\ $$$$\mathrm{equations}\:\mathrm{has}\:\mathrm{four}\:\mathrm{solutions}: \\ $$$$\left(\mathrm{x};\mathrm{y}\right)\in\left\{\left(\mathrm{x}_{\mathrm{1}} ;\mathrm{y}_{\mathrm{1}} \right);\left(\mathrm{x}_{\mathrm{2}} ;\mathrm{y}_{\mathrm{2}} \right);\left(\mathrm{x}_{\mathrm{3}} ,\mathrm{y}_{\mathrm{3}} \right);\left(\mathrm{x}_{\mathrm{4}} ;\mathrm{y}_{\mathrm{4}} \right)\right\} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\left[\:\frac{\mathrm{y}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:+\:\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:\right]\:\mathrm{dx}\:+\:\left[\frac{\mathrm{y}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }−\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:\right]\mathrm{dy}=\mathrm{0} \\ $$
Commented by I want to learn more last updated on 23/May/20

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
