Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 9485 by Joel575 last updated on 10/Dec/16

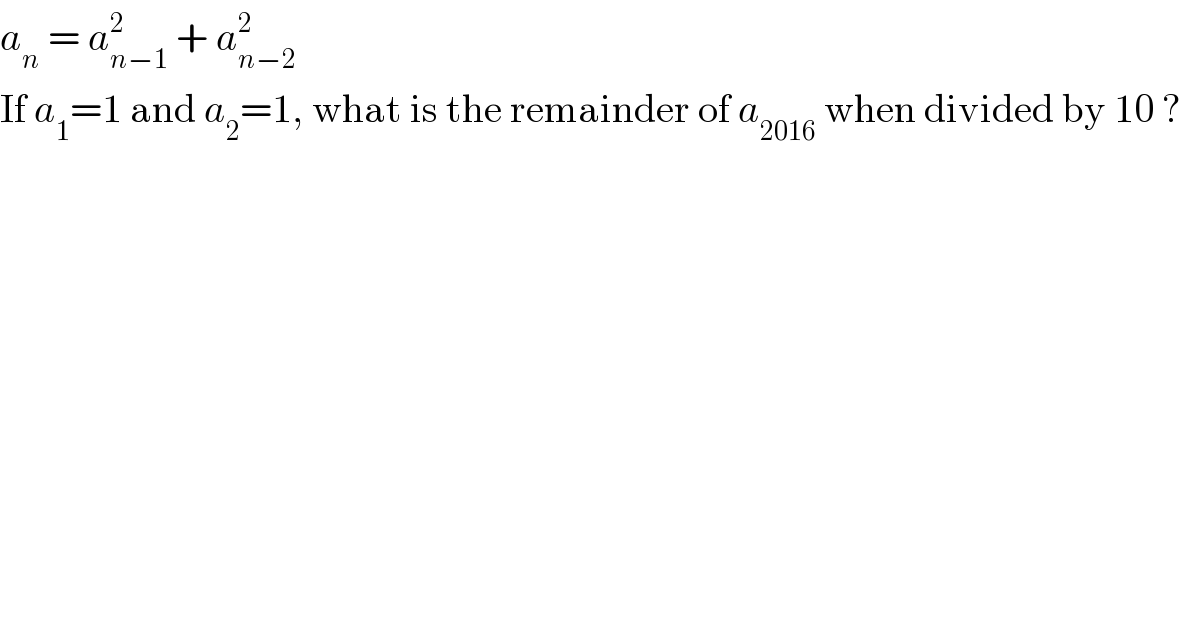
a_n = a_(n−1) ^2 + a_(n−2) ^2 If a_1 =1 and a_2 =1, what is the remainder of a_(2016) when divided by 10 ?

$${a}_{{n}} \:=\:{a}_{{n}−\mathrm{1}} ^{\mathrm{2}} \:+\:{a}_{{n}−\mathrm{2}} ^{\mathrm{2}} \\ $$$$\mathrm{If}\:{a}_{\mathrm{1}} =\mathrm{1}\:\mathrm{and}\:{a}_{\mathrm{2}} =\mathrm{1},\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{of}\:{a}_{\mathrm{2016}} \:\mathrm{when}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{10}\:? \\ $$

Commented by sou1618 last updated on 10/Dec/16

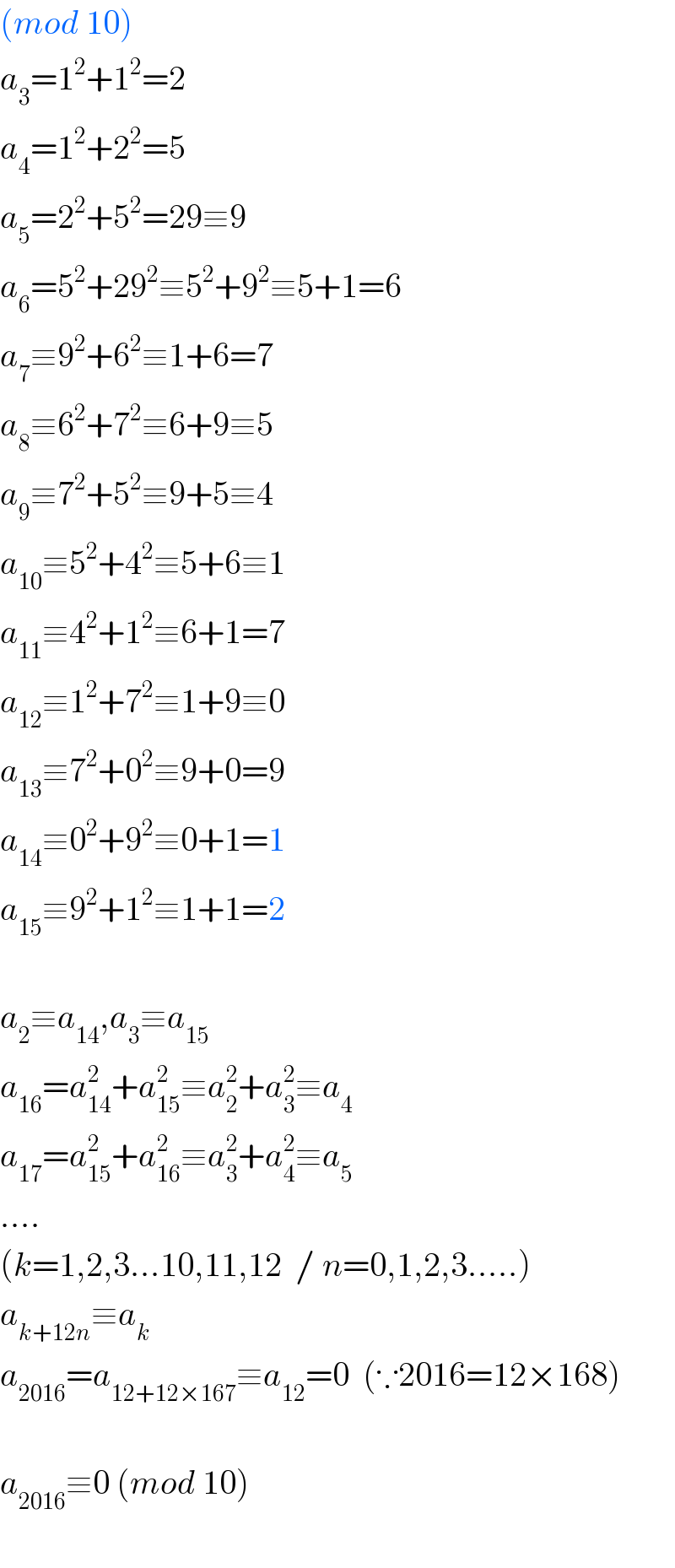
(mod 10) a_3 =1^2 +1^2 =2 a_4 =1^2 +2^2 =5 a_5 =2^2 +5^2 =29≡9 a_6 =5^2 +29^2 ≡5^2 +9^2 ≡5+1=6 a_7 ≡9^2 +6^2 ≡1+6=7 a_8 ≡6^2 +7^2 ≡6+9≡5 a_9 ≡7^2 +5^2 ≡9+5≡4 a_(10) ≡5^2 +4^2 ≡5+6≡1 a_(11) ≡4^2 +1^2 ≡6+1=7 a_(12) ≡1^2 +7^2 ≡1+9≡0 a_(13) ≡7^2 +0^2 ≡9+0=9 a_(14) ≡0^2 +9^2 ≡0+1=1 a_(15) ≡9^2 +1^2 ≡1+1=2 a_2 ≡a_(14) ,a_3 ≡a_(15) a_(16) =a_(14) ^2 +a_(15) ^2 ≡a_2 ^2 +a_3 ^2 ≡a_4 a_(17) =a_(15) ^2 +a_(16) ^2 ≡a_3 ^2 +a_4 ^2 ≡a_5 .... (k=1,2,3...10,11,12 / n=0,1,2,3.....) a_(k+12n) ≡a_k a_(2016) =a_(12+12×167) ≡a_(12) =0 (∵2016=12×168) a_(2016) ≡0 (mod 10)

$$\left({mod}\:\mathrm{10}\right) \\ $$$${a}_{\mathrm{3}} =\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} =\mathrm{2} \\ $$$${a}_{\mathrm{4}} =\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} =\mathrm{5} \\ $$$${a}_{\mathrm{5}} =\mathrm{2}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} =\mathrm{29}\equiv\mathrm{9} \\ $$$${a}_{\mathrm{6}} =\mathrm{5}^{\mathrm{2}} +\mathrm{29}^{\mathrm{2}} \equiv\mathrm{5}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} \equiv\mathrm{5}+\mathrm{1}=\mathrm{6} \\ $$$${a}_{\mathrm{7}} \equiv\mathrm{9}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} \equiv\mathrm{1}+\mathrm{6}=\mathrm{7} \\ $$$${a}_{\mathrm{8}} \equiv\mathrm{6}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} \equiv\mathrm{6}+\mathrm{9}\equiv\mathrm{5} \\ $$$${a}_{\mathrm{9}} \equiv\mathrm{7}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \equiv\mathrm{9}+\mathrm{5}\equiv\mathrm{4} \\ $$$${a}_{\mathrm{10}} \equiv\mathrm{5}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} \equiv\mathrm{5}+\mathrm{6}\equiv\mathrm{1} \\ $$$${a}_{\mathrm{11}} \equiv\mathrm{4}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} \equiv\mathrm{6}+\mathrm{1}=\mathrm{7} \\ $$$${a}_{\mathrm{12}} \equiv\mathrm{1}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} \equiv\mathrm{1}+\mathrm{9}\equiv\mathrm{0} \\ $$$${a}_{\mathrm{13}} \equiv\mathrm{7}^{\mathrm{2}} +\mathrm{0}^{\mathrm{2}} \equiv\mathrm{9}+\mathrm{0}=\mathrm{9} \\ $$$${a}_{\mathrm{14}} \equiv\mathrm{0}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} \equiv\mathrm{0}+\mathrm{1}=\mathrm{1} \\ $$$${a}_{\mathrm{15}} \equiv\mathrm{9}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} \equiv\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$$$ \\ $$$${a}_{\mathrm{2}} \equiv{a}_{\mathrm{14}} ,{a}_{\mathrm{3}} \equiv{a}_{\mathrm{15}} \\ $$$${a}_{\mathrm{16}} ={a}_{\mathrm{14}} ^{\mathrm{2}} +{a}_{\mathrm{15}} ^{\mathrm{2}} \equiv{a}_{\mathrm{2}} ^{\mathrm{2}} +{a}_{\mathrm{3}} ^{\mathrm{2}} \equiv{a}_{\mathrm{4}} \\ $$$${a}_{\mathrm{17}} ={a}_{\mathrm{15}} ^{\mathrm{2}} +{a}_{\mathrm{16}} ^{\mathrm{2}} \equiv{a}_{\mathrm{3}} ^{\mathrm{2}} +{a}_{\mathrm{4}} ^{\mathrm{2}} \equiv{a}_{\mathrm{5}} \\ $$$$.... \\ $$$$\left({k}=\mathrm{1},\mathrm{2},\mathrm{3}...\mathrm{10},\mathrm{11},\mathrm{12}\:\:/\:{n}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3}.....\right) \\ $$$${a}_{{k}+\mathrm{12}{n}} \equiv{a}_{{k}} \\ $$$${a}_{\mathrm{2016}} ={a}_{\mathrm{12}+\mathrm{12}×\mathrm{167}} \equiv{a}_{\mathrm{12}} =\mathrm{0}\:\:\left(\because\mathrm{2016}=\mathrm{12}×\mathrm{168}\right) \\ $$$$ \\ $$$${a}_{\mathrm{2016}} \equiv\mathrm{0}\:\left({mod}\:\mathrm{10}\right) \\ $$$$ \\ $$

Commented by Joel575 last updated on 11/Dec/16

thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com