
Question Number 9482 by sou1618 last updated on 10/Dec/16
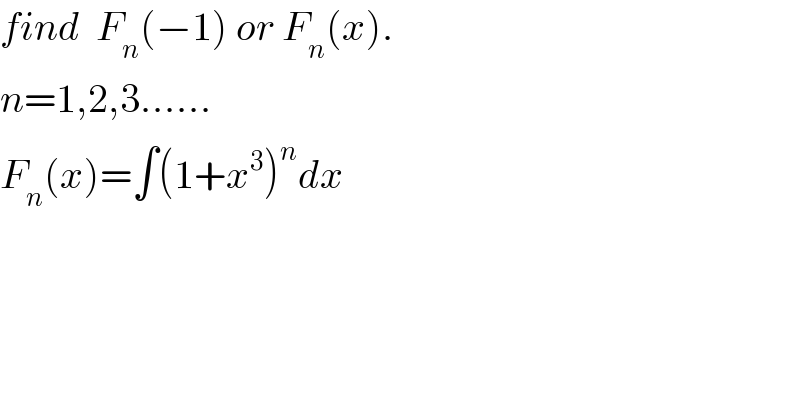
$${find}\:\:{F}_{{n}} \left(−\mathrm{1}\right)\:{or}\:{F}_{{n}} \left({x}\right). \\ $$$${n}=\mathrm{1},\mathrm{2},\mathrm{3}...... \\ $$$${F}_{{n}} \left({x}\right)=\int\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{{n}} {dx} \\ $$
Commented by sou1618 last updated on 10/Dec/16
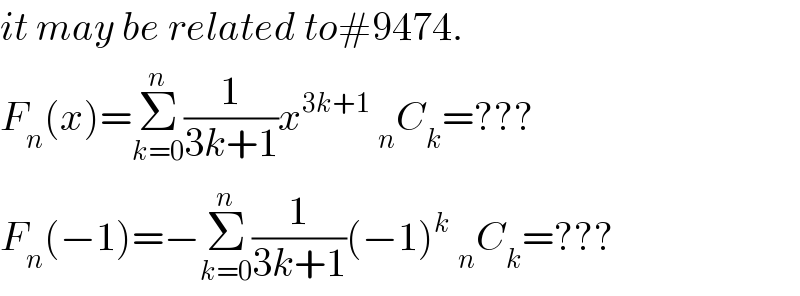
$${it}\:{may}\:{be}\:{related}\:{to}#\mathrm{9474}. \\ $$$${F}_{{n}} \left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{3}{k}+\mathrm{1}}{x}^{\mathrm{3}{k}+\mathrm{1}} \:_{{n}} {C}_{{k}} =??? \\ $$$${F}_{{n}} \left(−\mathrm{1}\right)=−\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{3}{k}+\mathrm{1}}\left(−\mathrm{1}\right)^{{k}} \:_{{n}} {C}_{{k}} =??? \\ $$
