
Question Number 94456 by Abdulrahman last updated on 18/May/20
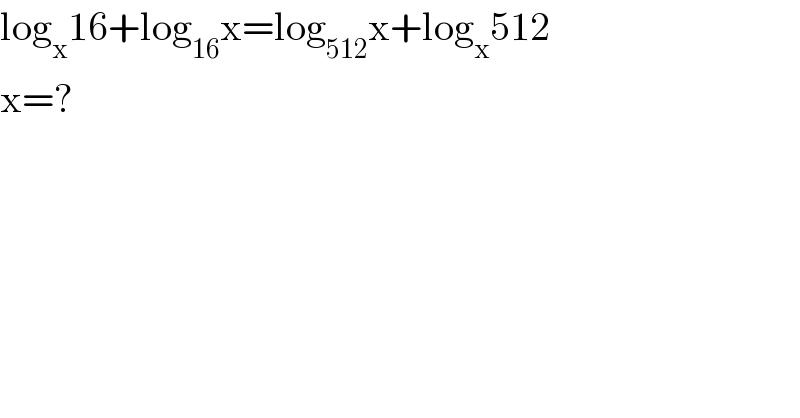
$$\mathrm{log}_{\mathrm{x}} \mathrm{16}+\mathrm{log}_{\mathrm{16}} \mathrm{x}=\mathrm{log}_{\mathrm{512}} \mathrm{x}+\mathrm{log}_{\mathrm{x}} \mathrm{512} \\ $$$$\mathrm{x}=? \\ $$
Answered by john santu last updated on 19/May/20
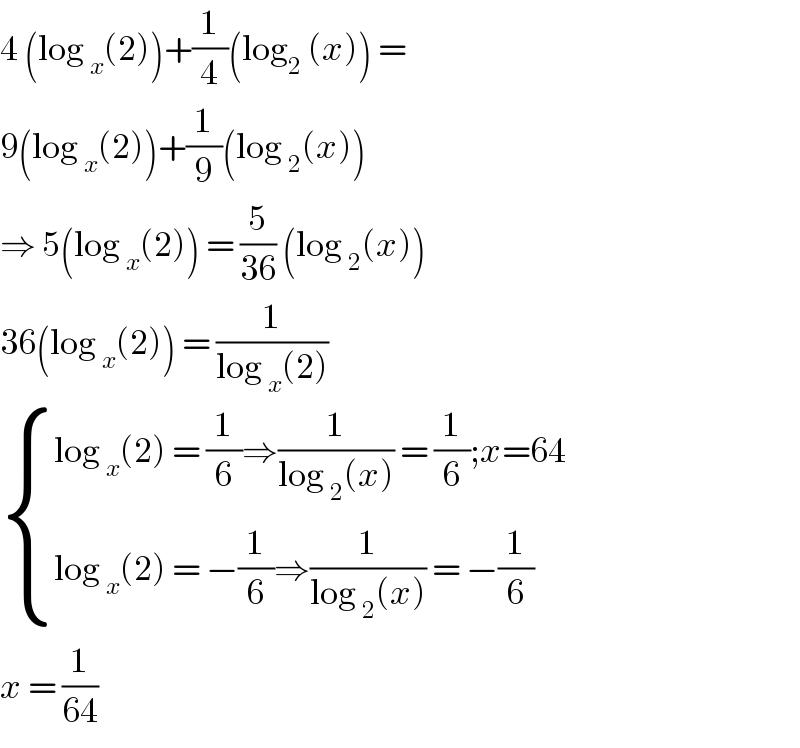
$$\mathrm{4}\:\left(\mathrm{log}\:_{{x}} \left(\mathrm{2}\right)\right)+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{log}_{\mathrm{2}} \:\left({x}\right)\right)\:=\: \\ $$$$\mathrm{9}\left(\mathrm{log}\:_{{x}} \left(\mathrm{2}\right)\right)+\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{log}\:_{\mathrm{2}} \left({x}\right)\right) \\ $$$$\Rightarrow\:\mathrm{5}\left(\mathrm{log}\:_{{x}} \left(\mathrm{2}\right)\right)\:=\:\frac{\mathrm{5}}{\mathrm{36}}\:\left(\mathrm{log}\:_{\mathrm{2}} \left({x}\right)\right) \\ $$$$\mathrm{36}\left(\mathrm{log}\:_{{x}} \left(\mathrm{2}\right)\right)\:=\:\frac{\mathrm{1}}{\mathrm{log}\:_{{x}} \left(\mathrm{2}\right)} \\ $$$$\begin{cases}{\mathrm{log}\:_{{x}} \left(\mathrm{2}\right)\:=\:\frac{\mathrm{1}}{\mathrm{6}}\Rightarrow\frac{\mathrm{1}}{\mathrm{log}\:_{\mathrm{2}} \left({x}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{6}};{x}=\mathrm{64}}\\{\mathrm{log}\:_{{x}} \left(\mathrm{2}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{6}}\Rightarrow\frac{\mathrm{1}}{\mathrm{log}\:_{\mathrm{2}} \left({x}\right)}\:=\:−\frac{\mathrm{1}}{\mathrm{6}}}\end{cases} \\ $$$${x}\:=\:\frac{\mathrm{1}}{\mathrm{64}} \\ $$
Commented by Abdulrahman last updated on 19/May/20
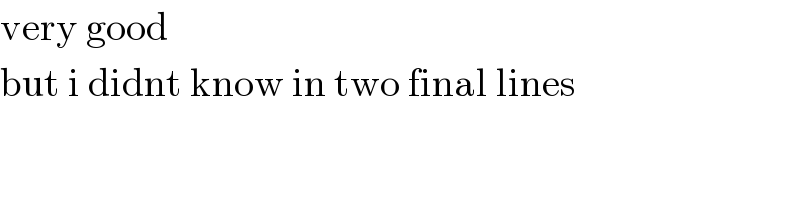
$$\mathrm{very}\:\mathrm{good} \\ $$$$\mathrm{but}\:\mathrm{i}\:\mathrm{didnt}\:\mathrm{know}\:\mathrm{in}\:\mathrm{two}\:\mathrm{final}\:\mathrm{lines} \\ $$
Commented by i jagooll last updated on 19/May/20

$$\mathrm{nice}\:\mathrm{solution} \\ $$
Commented by i jagooll last updated on 19/May/20
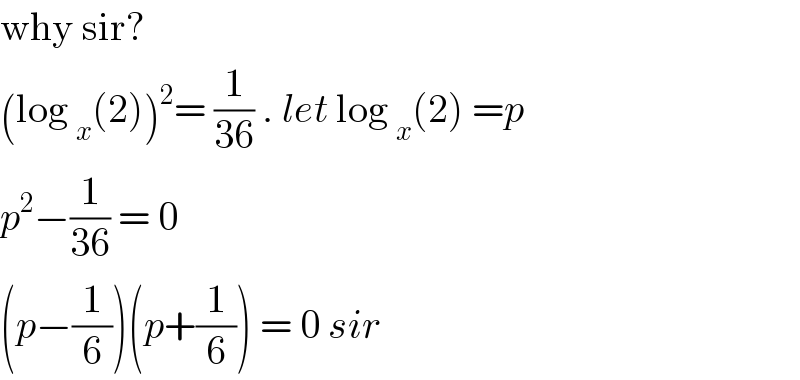
$$\mathrm{why}\:\mathrm{sir}?\: \\ $$$$\left(\mathrm{log}\:_{{x}} \left(\mathrm{2}\right)\right)^{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{36}}\:.\:{let}\:\mathrm{log}\:_{{x}} \left(\mathrm{2}\right)\:={p} \\ $$$${p}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{36}}\:=\:\mathrm{0} \\ $$$$\left({p}−\frac{\mathrm{1}}{\mathrm{6}}\right)\left({p}+\frac{\mathrm{1}}{\mathrm{6}}\right)\:=\:\mathrm{0}\:{sir} \\ $$
Commented by Abdulrahman last updated on 19/May/20
$$\mathrm{thanks}\:\mathrm{alot}\:\mathrm{now}\:\mathrm{i}\:\mathrm{got}\:\mathrm{it}\: \\ $$
