
Question Number 94424 by Abdulrahman last updated on 18/May/20

$$\mathrm{y}=\mathrm{x}^{\mathrm{x}} \\ $$$$\mathrm{y}^{'} =? \\ $$
Commented by Tony Lin last updated on 18/May/20

$${y}^{'} ={e}^{{xlnx}} \left({lnx}+\mathrm{1}\right) \\ $$$$\:\:\:={x}^{{x}} \left({lnx}+\mathrm{1}\right) \\ $$
Commented by PRITHWISH SEN 2 last updated on 18/May/20

$$\mathrm{y}^{'} =\mathrm{x}^{\mathrm{x}} \left(\mathrm{lnx}+\mathrm{1}\right) \\ $$
Commented by Abdulrahman last updated on 18/May/20

$$\mathrm{thanks} \\ $$
Commented by Abdulrahman last updated on 18/May/20

$$\mathrm{thankx} \\ $$
Answered by prakash jain last updated on 18/May/20
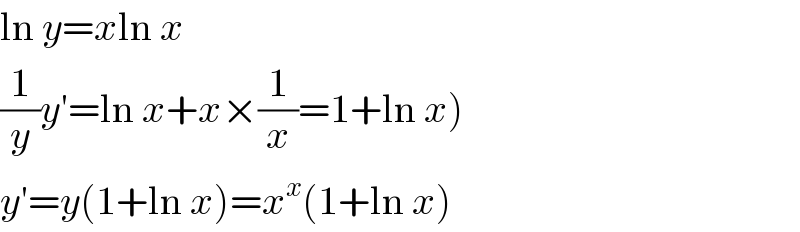
$$\mathrm{ln}\:{y}={x}\mathrm{ln}\:{x} \\ $$$$\left.\frac{\mathrm{1}}{{y}}{y}'=\mathrm{ln}\:{x}+{x}×\frac{\mathrm{1}}{{x}}=\mathrm{1}+\mathrm{ln}\:{x}\right) \\ $$$${y}'={y}\left(\mathrm{1}+\mathrm{ln}\:{x}\right)={x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right) \\ $$
Commented by Abdulrahman last updated on 18/May/20

$$\mathrm{thanks} \\ $$
