
Question Number 94419 by sorour87.d last updated on 18/May/20
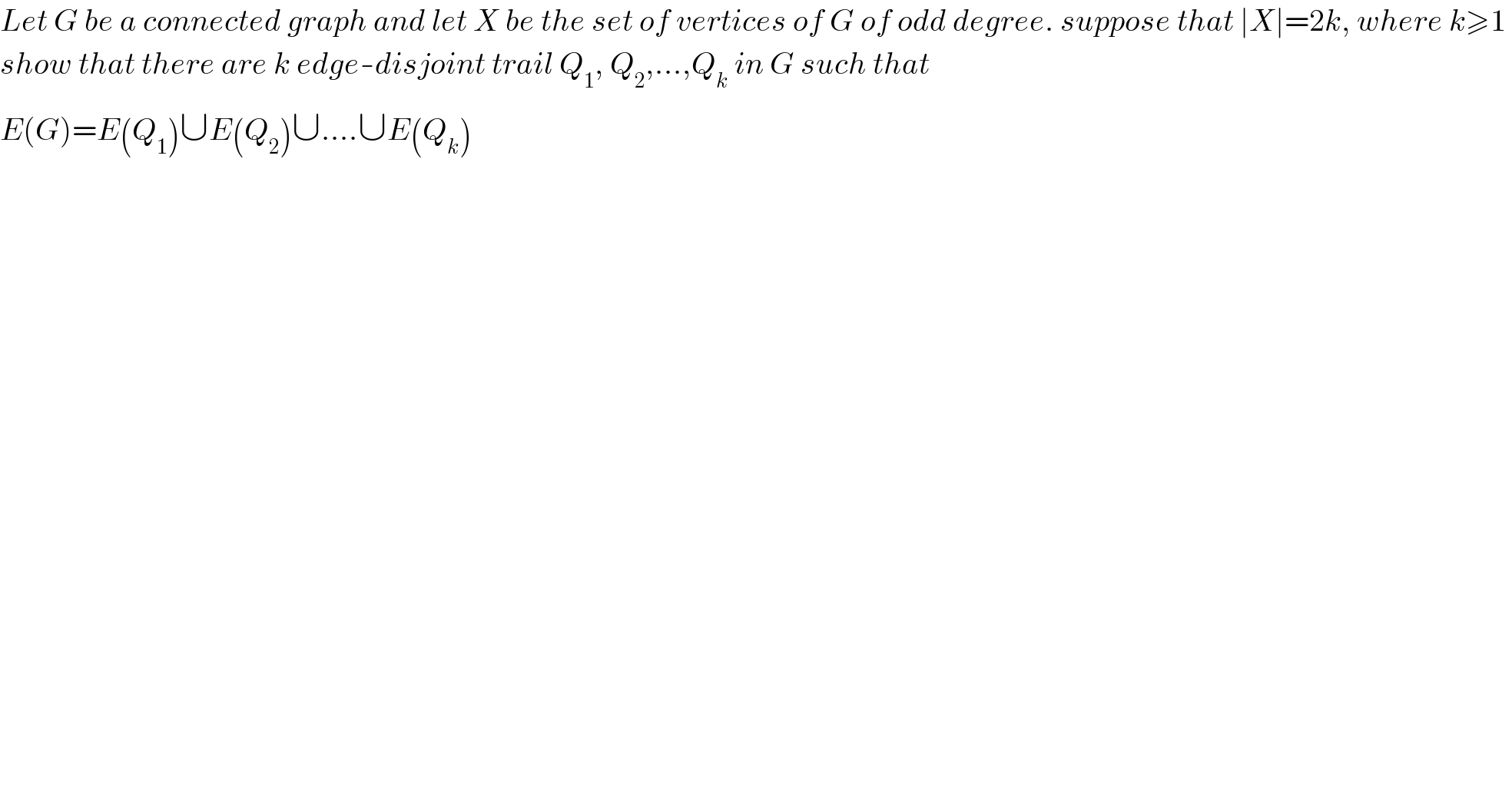
$${Let}\:{G}\:{be}\:{a}\:{connected}\:{graph}\:{and}\:{let}\:{X}\:{be}\:{the}\:{set}\:{of}\:{vertices}\:{of}\:{G}\:{of}\:{odd}\:{degree}.\:{suppose}\:{that}\:\mid{X}\mid=\mathrm{2}{k},\:{where}\:{k}\geqslant\mathrm{1}\: \\ $$$${show}\:{that}\:{there}\:{are}\:{k}\:{edge}-{disjoint}\:{trail}\:{Q}_{\mathrm{1}} ,\:{Q}_{\mathrm{2}} ,...,{Q}_{{k}} \:{in}\:{G}\:{such}\:{that} \\ $$$${E}\left({G}\right)={E}\left({Q}_{\mathrm{1}} \right)\cup{E}\left({Q}_{\mathrm{2}} \right)\cup....\cup{E}\left({Q}_{{k}} \right) \\ $$
