
Previous in Relation and Functions Next in Relation and Functions
Question Number 93908 by abdomathmax last updated on 16/May/20
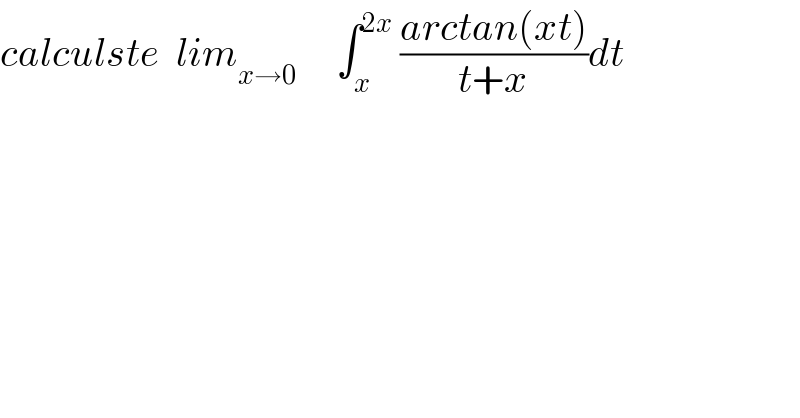
$${calculste}\:\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\int_{{x}} ^{\mathrm{2}{x}} \:\frac{{arctan}\left({xt}\right)}{{t}+{x}}{dt} \\ $$
Commented by redmiiuser last updated on 16/May/20

$${Answer}:\mathrm{0} \\ $$
Commented by abdomathmax last updated on 17/May/20
![let F(x)=∫_x ^(2x) ((arctan(xt))/(t+x)) dt we do the changement xt =u ⇒F(x) =∫_x^2 ^(2x^2 ) ((arctan(u))/((u/x) +x)) (du/x) =∫_x^2 ^(2x^2 ) ((arctanu)/(u+x^2 ))du ∃ c_x ∈]x^2 ,2x^2 [ / F(x) =arctsn(c_x )∫_x^2 ^(2x^2 ) (du/(u+x^2 )) =arctan(c_x )[ln(u+x^2 )]_x^2 ^(2x^2 ) =arctan(c_x )×(ln(((3x^2 )/(2x^2 )))) but x→0 ⇒c_x →0 ⇒ lim_(x→0) F(x) =0×ln((3/2)) =0](Q94149.png)
$${let}\:{F}\left({x}\right)=\int_{{x}} ^{\mathrm{2}{x}} \:\frac{{arctan}\left({xt}\right)}{{t}+{x}}\:{dt}\:{we}\:{do}\:{the}\:{changement} \\ $$$${xt}\:={u}\:\Rightarrow{F}\left({x}\right)\:=\int_{{x}^{\mathrm{2}} } ^{\mathrm{2}{x}^{\mathrm{2}} } \:\:\frac{{arctan}\left({u}\right)}{\frac{{u}}{{x}}\:+{x}}\:\frac{{du}}{{x}} \\ $$$$\left.=\int_{{x}^{\mathrm{2}} } ^{\mathrm{2}{x}^{\mathrm{2}} } \:\:\:\frac{{arctanu}}{{u}+{x}^{\mathrm{2}} }{du}\:\:\:\:\exists\:{c}_{{x}} \in\right]{x}^{\mathrm{2}} \:,\mathrm{2}{x}^{\mathrm{2}} \left[\:/\right. \\ $$$${F}\left({x}\right)\:={arctsn}\left({c}_{{x}} \right)\int_{{x}^{\mathrm{2}} } ^{\mathrm{2}{x}^{\mathrm{2}} } \:\frac{{du}}{{u}+{x}^{\mathrm{2}} }\:={arctan}\left({c}_{{x}} \right)\left[{ln}\left({u}+{x}^{\mathrm{2}} \right)\right]_{{x}^{\mathrm{2}} } ^{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$={arctan}\left({c}_{{x}} \right)×\left({ln}\left(\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }\right)\right)\:\:{but}\:{x}\rightarrow\mathrm{0}\:\Rightarrow{c}_{{x}} \rightarrow\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:{F}\left({x}\right)\:=\mathrm{0}×{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\mathrm{0} \\ $$
