
Question Number 93460 by john santu last updated on 13/May/20
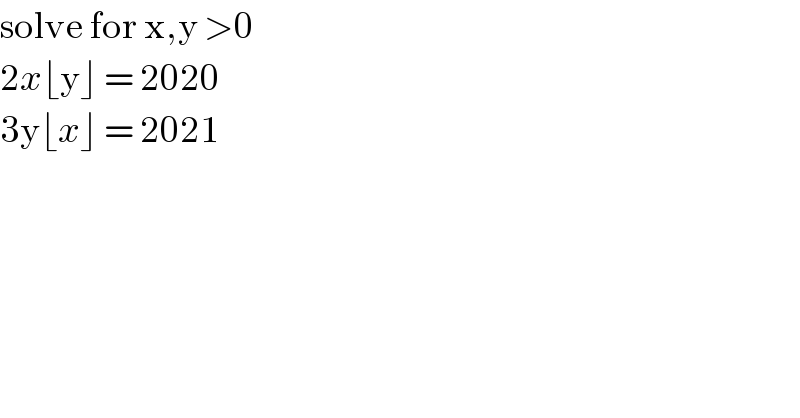
$$\mathrm{solve}\:\mathrm{for}\:\mathrm{x},\mathrm{y}\:>\mathrm{0} \\ $$ $$\mathrm{2}{x}\lfloor\mathrm{y}\rfloor\:=\:\mathrm{2020} \\ $$ $$\mathrm{3y}\lfloor{x}\rfloor\:=\:\mathrm{2021}\: \\ $$
Commented byjohn santu last updated on 13/May/20

$${ans}\::\:\left(\frac{\mathrm{1010}}{\mathrm{673}}\:,\:\frac{\mathrm{2021}}{\mathrm{3}}\right)\: \\ $$
Answered by mr W last updated on 16/May/20
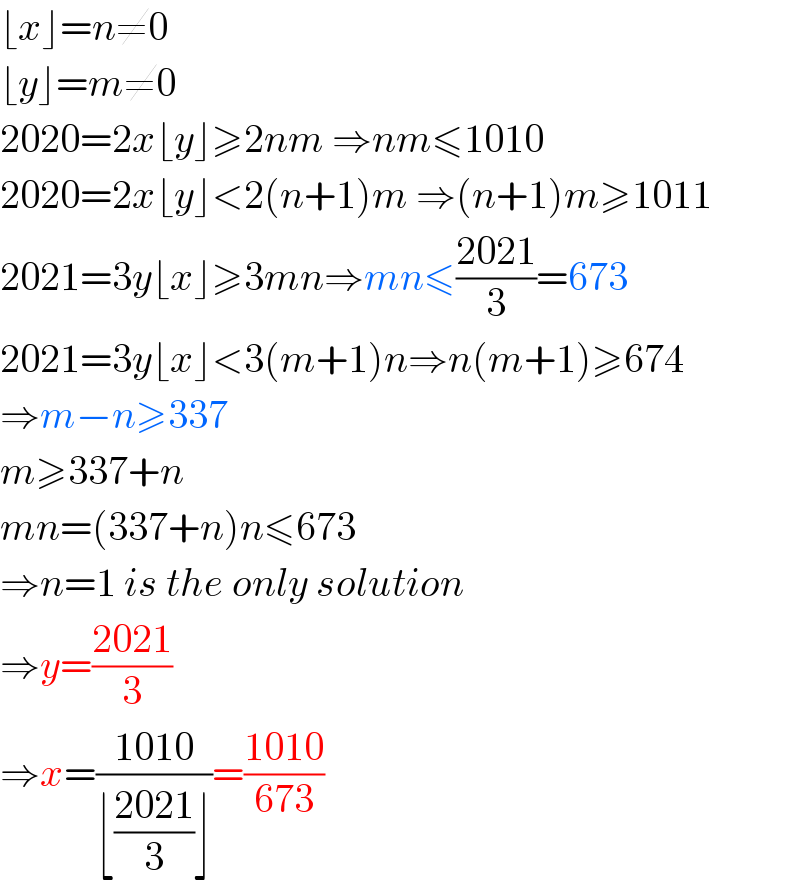
$$\lfloor{x}\rfloor={n}\neq\mathrm{0} \\ $$ $$\lfloor{y}\rfloor={m}\neq\mathrm{0} \\ $$ $$\mathrm{2020}=\mathrm{2}{x}\lfloor{y}\rfloor\geqslant\mathrm{2}{nm}\:\Rightarrow{nm}\leqslant\mathrm{1010} \\ $$ $$\mathrm{2020}=\mathrm{2}{x}\lfloor{y}\rfloor<\mathrm{2}\left({n}+\mathrm{1}\right){m}\:\Rightarrow\left({n}+\mathrm{1}\right){m}\geqslant\mathrm{1011} \\ $$ $$\mathrm{2021}=\mathrm{3}{y}\lfloor{x}\rfloor\geqslant\mathrm{3}{mn}\Rightarrow{mn}\leqslant\frac{\mathrm{2021}}{\mathrm{3}}=\mathrm{673} \\ $$ $$\mathrm{2021}=\mathrm{3}{y}\lfloor{x}\rfloor<\mathrm{3}\left({m}+\mathrm{1}\right){n}\Rightarrow{n}\left({m}+\mathrm{1}\right)\geqslant\mathrm{674} \\ $$ $$\Rightarrow{m}−{n}\geqslant\mathrm{337} \\ $$ $${m}\geqslant\mathrm{337}+{n} \\ $$ $${mn}=\left(\mathrm{337}+{n}\right){n}\leqslant\mathrm{673} \\ $$ $$\Rightarrow{n}=\mathrm{1}\:{is}\:{the}\:{only}\:{solution} \\ $$ $$\Rightarrow{y}=\frac{\mathrm{2021}}{\mathrm{3}} \\ $$ $$\Rightarrow{x}=\frac{\mathrm{1010}}{\lfloor\frac{\mathrm{2021}}{\mathrm{3}}\rfloor}=\frac{\mathrm{1010}}{\mathrm{673}} \\ $$
