
Question Number 93451 by mhmd last updated on 13/May/20
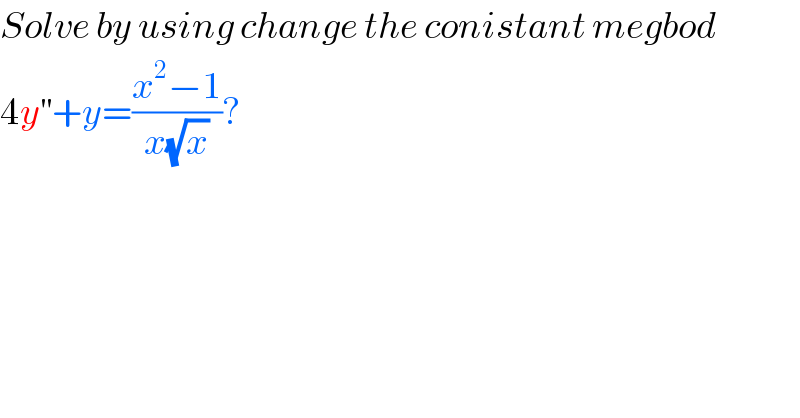
$${Solve}\:{by}\:{using}\:{change}\:{the}\:{conistant}\:{megbod}\: \\ $$$$\mathrm{4}{y}^{''} +{y}=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}\sqrt{{x}}}? \\ $$
Commented by i jagooll last updated on 13/May/20
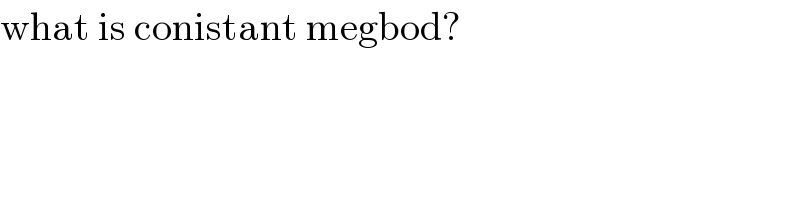
$$\mathrm{what}\:\mathrm{is}\:\mathrm{conistant}\:\mathrm{megbod}? \\ $$
Commented by mhmd last updated on 13/May/20
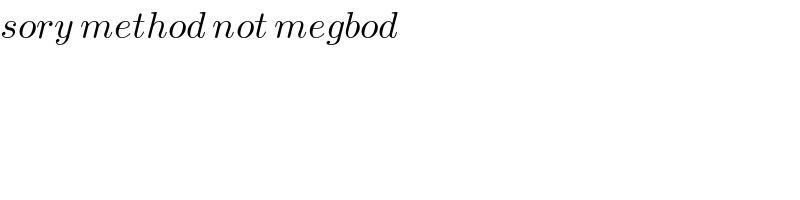
$${sory}\:{method}\:{not}\:{megbod} \\ $$
Commented by john santu last updated on 13/May/20

$$\mathrm{characteristic}\:\mathrm{eq}\::\:\mathrm{4r}^{\mathrm{2}} +\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{r}\:=\:\pm\:\frac{\mathrm{1}}{\mathrm{2}}\:{i}\:.\:\mathrm{homogenous}\:\mathrm{solution} \\ $$$$\mathrm{y}_{\mathrm{h}} =\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}{i}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}{i}} \\ $$$$\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)+\mathrm{C}_{\mathrm{2}} \mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right) \\ $$$$\mathrm{Particular}\:\mathrm{solution}\: \\ $$$$\mathrm{y}_{\mathrm{p}} \:=\frac{\sqrt{{x}}−{x}^{−\mathrm{3}/\mathrm{2}} }{\mathrm{4D}^{\mathrm{2}} +\mathrm{1}}\: \\ $$
