
Question Number 93241 by Ayod 19 last updated on 12/May/20
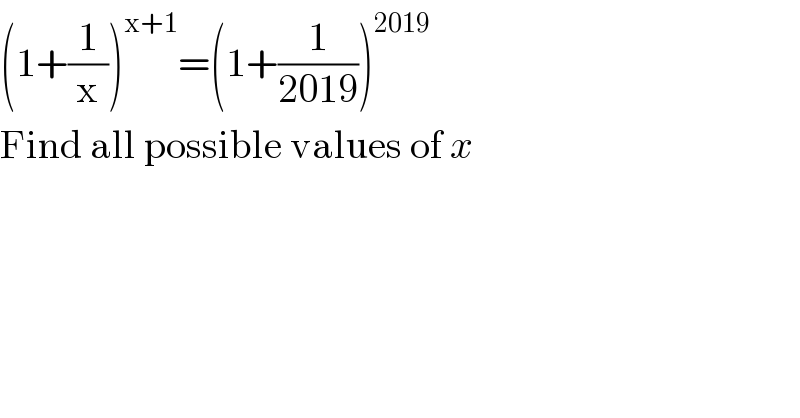
$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{x}+\mathrm{1}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2019}}\right)^{\mathrm{2019}} \\ $$$$\mathrm{Find}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{of}\:{x} \\ $$
Answered by prakash jain last updated on 12/May/20
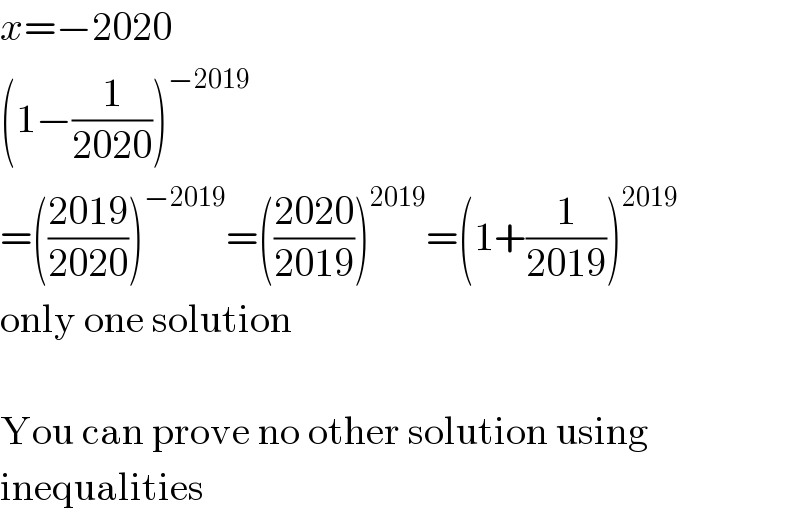
$${x}=−\mathrm{2020} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2020}}\right)^{−\mathrm{2019}} \\ $$$$=\left(\frac{\mathrm{2019}}{\mathrm{2020}}\right)^{−\mathrm{2019}} =\left(\frac{\mathrm{2020}}{\mathrm{2019}}\right)^{\mathrm{2019}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2019}}\right)^{\mathrm{2019}} \\ $$$$\mathrm{only}\:\mathrm{one}\:\mathrm{solution} \\ $$$$ \\ $$$$\mathrm{You}\:\mathrm{can}\:\mathrm{prove}\:\mathrm{no}\:\mathrm{other}\:\mathrm{solution}\:\mathrm{using} \\ $$$$\mathrm{inequalities} \\ $$
