
Question Number 92484 by jagoll last updated on 07/May/20
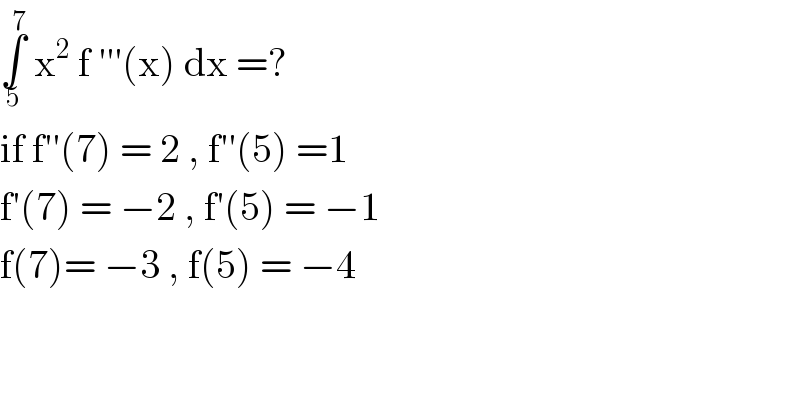
$$\underset{\mathrm{5}} {\overset{\mathrm{7}} {\int}}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{f}\:'''\left(\mathrm{x}\right)\:\mathrm{dx}\:=? \\ $$$$\mathrm{if}\:\mathrm{f}''\left(\mathrm{7}\right)\:=\:\mathrm{2}\:,\:\mathrm{f}''\left(\mathrm{5}\right)\:=\mathrm{1} \\ $$$$\mathrm{f}'\left(\mathrm{7}\right)\:=\:−\mathrm{2}\:,\:\mathrm{f}'\left(\mathrm{5}\right)\:=\:−\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{7}\right)=\:−\mathrm{3}\:,\:\mathrm{f}\left(\mathrm{5}\right)\:=\:−\mathrm{4}\: \\ $$$$ \\ $$
Answered by john santu last updated on 07/May/20
![D.I method ∫_5 ^7 x^(2 ) f′′′(x) dx = x^2 f′′(x) − 2x f′(x)+2f(x) ]_5 ^7 = 49f′′(7)−25f′′(5)−{14f′(7)−10f′(5) +2f(7)−2f(5) = 98−25−{−28+10}+(−6+8) = 73+18+2 = 93](Q92485.png)
$$\mathrm{D}.\mathrm{I}\:\mathrm{method}\: \\ $$$$\left.\underset{\mathrm{5}} {\overset{\mathrm{7}} {\int}}\:\mathrm{x}^{\mathrm{2}\:} \mathrm{f}'''\left(\mathrm{x}\right)\:\mathrm{dx}\:=\:\mathrm{x}^{\mathrm{2}} \:\mathrm{f}''\left(\mathrm{x}\right)\:−\:\mathrm{2x}\:\mathrm{f}'\left(\mathrm{x}\right)+\mathrm{2f}\left(\mathrm{x}\right)\:\right]_{\mathrm{5}} ^{\mathrm{7}} \\ $$$$=\:\mathrm{49f}''\left(\mathrm{7}\right)−\mathrm{25f}''\left(\mathrm{5}\right)−\left\{\mathrm{14f}'\left(\mathrm{7}\right)−\mathrm{10f}'\left(\mathrm{5}\right)\right. \\ $$$$+\mathrm{2f}\left(\mathrm{7}\right)−\mathrm{2f}\left(\mathrm{5}\right) \\ $$$$=\:\mathrm{98}−\mathrm{25}−\left\{−\mathrm{28}+\mathrm{10}\right\}+\left(−\mathrm{6}+\mathrm{8}\right) \\ $$$$=\:\mathrm{73}+\mathrm{18}+\mathrm{2}\:=\:\mathrm{93} \\ $$
Commented by jagoll last updated on 07/May/20
������
