
Question Number 92465 by Rio Michael last updated on 07/May/20
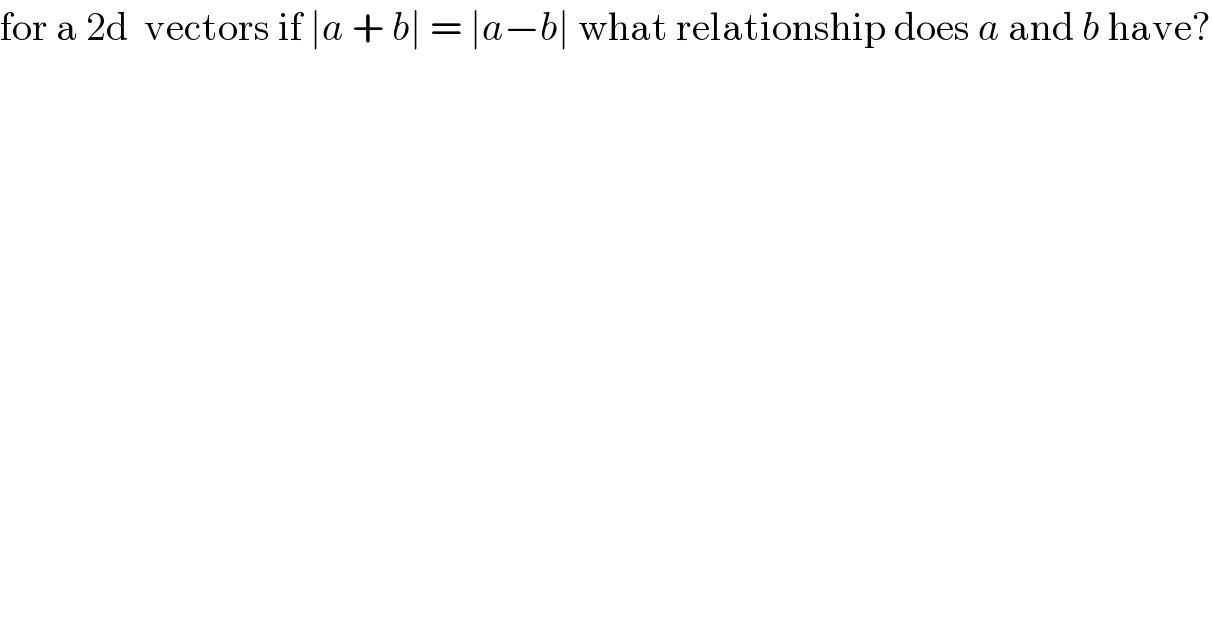
$$\mathrm{for}\:\mathrm{a}\:\mathrm{2d}\:\:\mathrm{vectors}\:\mathrm{if}\:\mid{a}\:+\:{b}\mid\:=\:\mid{a}−{b}\mid\:\mathrm{what}\:\mathrm{relationship}\:\mathrm{does}\:{a}\:\mathrm{and}\:{b}\:\mathrm{have}? \\ $$$$ \\ $$
Commented by mr W last updated on 07/May/20

$$\boldsymbol{{a}}\bot\boldsymbol{{b}} \\ $$
Commented by Rio Michael last updated on 07/May/20
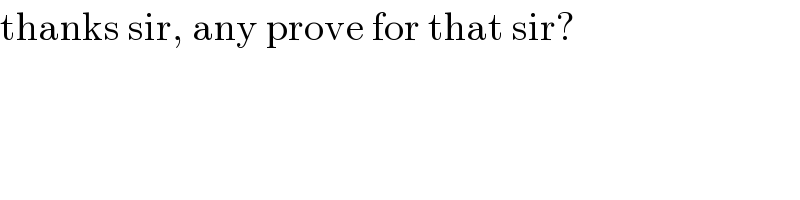
$$\mathrm{thanks}\:\mathrm{sir},\:\mathrm{any}\:\mathrm{prove}\:\mathrm{for}\:\mathrm{that}\:\mathrm{sir}? \\ $$
Commented by mr W last updated on 07/May/20

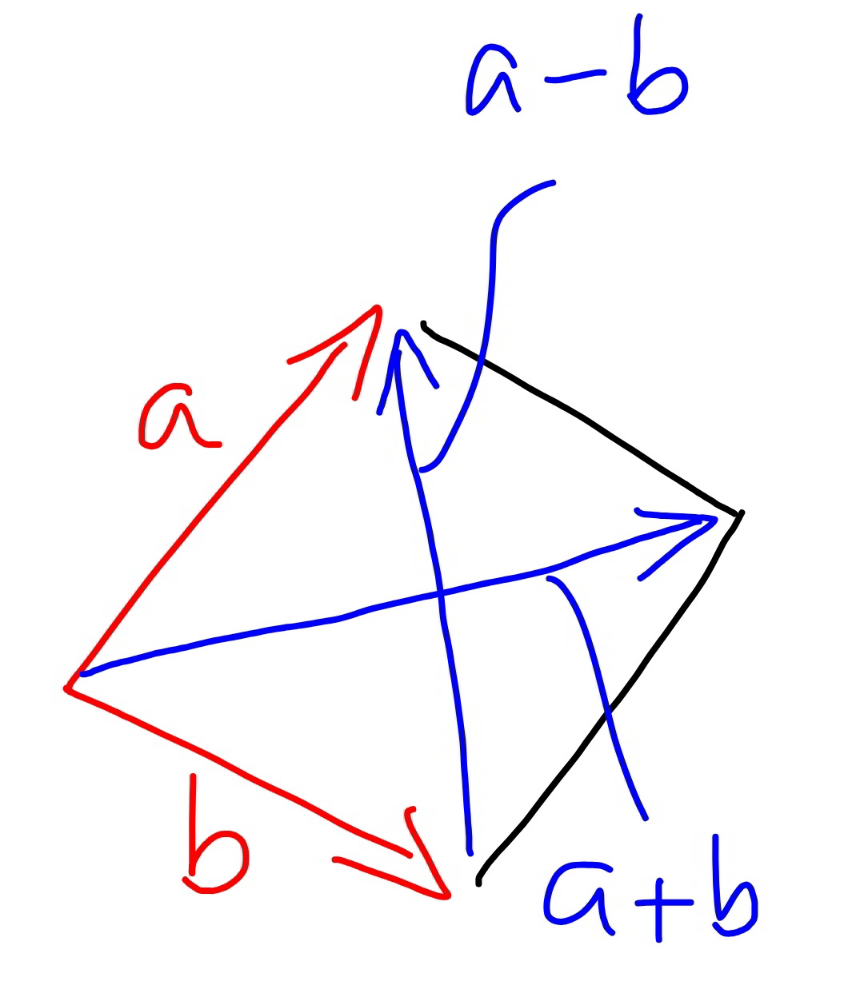
$$\mid{a}+{b}\mid\:{and}\:\mid{a}−{b}\mid\:{are}\:{the}\:{both}\:{diagonals} \\ $$$${of}\:{the}\:{paralleogram}\:{with}\:{a}\:{and}\:{b}\:{as} \\ $$$${sides}.\:{when}\:{both}\:{diagonals}\:{should}\:{be} \\ $$$${equal},\:{the}\:{parallelogram}\:{must}\:{be}\:{a} \\ $$$${rectangle},\:{i}.{e}.\:{a}\:{and}\:{b}\:{must}\:{be}\:\bot\:{to} \\ $$$${each}\:{other}. \\ $$
Commented by mr W last updated on 13/May/20
Commented by Rio Michael last updated on 07/May/20
$$\mathrm{following}\:\mathrm{your}\:\mathrm{explanation}\:\mathrm{i}\:\mathrm{checked}\:\mathrm{that} \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Prithwish Sen 1 last updated on 07/May/20

$$\because\:\:\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}\:\mathrm{and}\:\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{b}}\:\mathrm{are}\:\mathrm{the}\:\mathrm{two}\:\mathrm{diagonals}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{parallalogram}\:\mathrm{formed}\:\mathrm{by}\:\mathrm{the}\:\mathrm{vectors}\:\boldsymbol{\mathrm{a}}\:\mathrm{and}\:\boldsymbol{\mathrm{b}} \\ $$$$\mathrm{as}\:\mathrm{the}\:\mathrm{two}\:\mathrm{adjacent}\:\mathrm{sides}\:\mathrm{then}\:\mathrm{if}\:\mid\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}\mid=\mid\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{b}}\mid \\ $$$$\mathrm{only}\:\mathrm{implies}\:\mathrm{that}\:\mathrm{the}\:\mathrm{diagonals}\:\mathrm{are}\:\mathrm{same}\:\mathrm{and}\:\mathrm{it} \\ $$$$\mathrm{can}\:\mathrm{only}\:\mathrm{happen}\:\mathrm{when}\:\mathrm{the}\:\mathrm{parallalogram}\:\mathrm{so}\: \\ $$$$\mathrm{formed}\:\mathrm{by}\:\boldsymbol{\mathrm{a}}\:\mathrm{and}\:\boldsymbol{\mathrm{b}}\:\mathrm{is}\:\mathrm{a}\:\boldsymbol{\mathrm{rectangle}}.\:\mathrm{And}\:\mathrm{that}\:\mathrm{is}\:\mathrm{why} \\ $$$$\mathrm{the}\:\mathrm{two}\:\mathrm{adjacent}\:\mathrm{sides}\:\mathrm{must}\:\mathrm{be}\:\bot\:\mathrm{and}\:\mathrm{i}.\mathrm{e}\: \\ $$$$\boldsymbol{\mathrm{a}}\bot\boldsymbol{\mathrm{b}}. \\ $$
Commented by Rio Michael last updated on 07/May/20
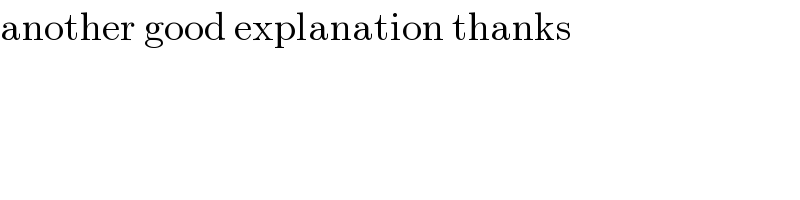
$$\mathrm{another}\:\mathrm{good}\:\mathrm{explanation}\:\mathrm{thanks} \\ $$
Answered by behi83417@gmail.com last updated on 07/May/20
![∣a+b∣=(√(a^2 +b^2 −2abcosθ)) ∣a−b∣=(√(a^2 +b^2 +2abcosθ)) [θ=angle between a and b] ∣a+b∣=∣a−b∣⇒ a^2 +b^2 −2abcosθ=a^2 +b^2 +2abcosθ ⇒4abcosθ=0⇒ { ((a=0 (or))),((b=0 (or))),((cosθ=0⇒θ=(π/2)⇒a⊥b)) :}](Q92523.png)
$$\mid\mathrm{a}+\mathrm{b}\mid=\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2abcos}\theta} \\ $$$$\mid\mathrm{a}−\mathrm{b}\mid=\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2abcos}\theta} \\ $$$$\left[\theta=\mathrm{angle}\:\mathrm{between}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b}\right] \\ $$$$\mid\mathrm{a}+\mathrm{b}\mid=\mid\mathrm{a}−\mathrm{b}\mid\Rightarrow \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2abcos}\theta=\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2abcos}\theta \\ $$$$\Rightarrow\mathrm{4abcos}\theta=\mathrm{0}\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{0}\:\:\left(\mathrm{or}\right)}\\{\mathrm{b}=\mathrm{0}\:\:\left(\mathrm{or}\right)}\\{\mathrm{cos}\theta=\mathrm{0}\Rightarrow\theta=\frac{\pi}{\mathrm{2}}\Rightarrow\mathrm{a}\bot\mathrm{b}}\end{cases} \\ $$
