
Question Number 9231 by tawakalitu last updated on 24/Nov/16
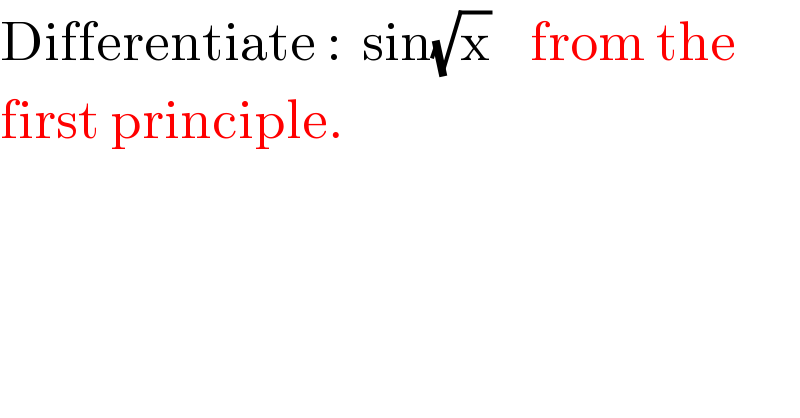
$$\mathrm{Differentiate}\::\:\:\mathrm{sin}\sqrt{\mathrm{x}}\:\:\:\:\mathrm{from}\:\mathrm{the} \\ $$$$\mathrm{first}\:\mathrm{principle}. \\ $$
Answered by mrW last updated on 29/Nov/16
![y(x)=sin (√x) y(x+h)=sin (√(x+h)) ((y(x+h)−y(x))/h)=((sin (√(x+h))−sin (√x))/h) =((2×cos (((√(x+h))+(√x))/2)×sin (((√(x+h))−(√x))/2))/h) =2×cos (((√(x+h))+(√x))/2)×((sin (((√(x+h))−(√x))/2))/h) let u=(((√(x+h))−(√x))/2) (√(x+h))−(√x)=2u (√(x+h))=2u+(√x) h=(2u+(√x))^2 −((√x))^2 =4u(u+(√x)) ((sin (((√(x+h))−(√x))/2))/h)=((sin u)/(4u(u+(√(x)))))=(1/4)×((sin u)/u)×(1/(u+(√x))) with h→0, u→0 lim_(h→0) ((sin (((√(x+h))−(√x))/2))/h)=(1/4)×lim_(u→0) ((sin u)/u)×lim_(u→0) (1/( u+(√x) ))=(1/4)×1×(1/(√x))=(1/(4(√x))) (dy/dx)=lim_(h→0) ((y(x+h)−y(x))/h) =lim_(h→0) [2×cos (((√(x+h))+(√x))/2)×((sin (((√(x+h))−(√x))/2))/h)] =2×lim_(h→0) cos (((√(x+h))+(√x))/2)×lim_(h→0) ((sin (((√(x+h))−(√x))/2))/h) =2×cos (√x)×(1/(4(√x)))=((cos (√x))/(2(√x)))](Q9310.png)
$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{sin}\:\sqrt{\mathrm{x}} \\ $$$$\mathrm{y}\left(\mathrm{x}+\mathrm{h}\right)=\mathrm{sin}\:\sqrt{\mathrm{x}+\mathrm{h}} \\ $$$$\frac{\mathrm{y}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{y}\left(\mathrm{x}\right)}{\mathrm{h}}=\frac{\mathrm{sin}\:\sqrt{\mathrm{x}+\mathrm{h}}−\mathrm{sin}\:\sqrt{\mathrm{x}}}{\mathrm{h}} \\ $$$$=\frac{\mathrm{2}×\mathrm{cos}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}}+\sqrt{\mathrm{x}}}{\mathrm{2}}×\mathrm{sin}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}}−\sqrt{\mathrm{x}}}{\mathrm{2}}}{\mathrm{h}} \\ $$$$=\mathrm{2}×\mathrm{cos}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}}+\sqrt{\mathrm{x}}}{\mathrm{2}}×\frac{\mathrm{sin}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}}−\sqrt{\mathrm{x}}}{\mathrm{2}}}{\mathrm{h}} \\ $$$$ \\ $$$$\mathrm{let}\:\mathrm{u}=\frac{\sqrt{\mathrm{x}+\mathrm{h}}−\sqrt{\mathrm{x}}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{x}+\mathrm{h}}−\sqrt{\mathrm{x}}=\mathrm{2u} \\ $$$$\sqrt{\mathrm{x}+\mathrm{h}}=\mathrm{2u}+\sqrt{\mathrm{x}} \\ $$$$\mathrm{h}=\left(\mathrm{2u}+\sqrt{\mathrm{x}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{x}}\right)^{\mathrm{2}} =\mathrm{4u}\left(\mathrm{u}+\sqrt{\mathrm{x}}\right) \\ $$$$ \\ $$$$\frac{\mathrm{sin}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}}−\sqrt{\mathrm{x}}}{\mathrm{2}}}{\mathrm{h}}=\frac{\mathrm{sin}\:\mathrm{u}}{\mathrm{4u}\left(\mathrm{u}+\sqrt{\left.\mathrm{x}\right)}\right.}=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{sin}\:\mathrm{u}}{\mathrm{u}}×\frac{\mathrm{1}}{\mathrm{u}+\sqrt{\mathrm{x}}} \\ $$$$ \\ $$$$\mathrm{with}\:\mathrm{h}\rightarrow\mathrm{0},\:\mathrm{u}\rightarrow\mathrm{0} \\ $$$$\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}}−\sqrt{\mathrm{x}}}{\mathrm{2}}}{\mathrm{h}}=\frac{\mathrm{1}}{\mathrm{4}}×\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{u}}{\mathrm{u}}×\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\:\mathrm{u}+\sqrt{\mathrm{x}}\:}=\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{1}×\frac{\mathrm{1}}{\sqrt{\mathrm{x}}}=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{x}}} \\ $$$$ \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{y}\left(\mathrm{x}+\mathrm{h}\right)−\mathrm{y}\left(\mathrm{x}\right)}{\mathrm{h}} \\ $$$$=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\mathrm{2}×\mathrm{cos}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}}+\sqrt{\mathrm{x}}}{\mathrm{2}}×\frac{\mathrm{sin}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}}−\sqrt{\mathrm{x}}}{\mathrm{2}}}{\mathrm{h}}\right] \\ $$$$=\mathrm{2}×\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}cos}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}}+\sqrt{\mathrm{x}}}{\mathrm{2}}×\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\frac{\sqrt{\mathrm{x}+\mathrm{h}}−\sqrt{\mathrm{x}}}{\mathrm{2}}}{\mathrm{h}} \\ $$$$=\mathrm{2}×\mathrm{cos}\:\sqrt{\mathrm{x}}×\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{x}}}=\frac{\boldsymbol{\mathrm{cos}}\:\sqrt{\boldsymbol{\mathrm{x}}}}{\mathrm{2}\sqrt{\boldsymbol{\mathrm{x}}}} \\ $$
Commented by tawakalitu last updated on 29/Nov/16
$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
