
Question Number 92196 by I want to learn more last updated on 05/May/20

$$\mathrm{2}^{\mathrm{x}} \:\:+\:\:\mathrm{3}^{\mathrm{y}} \:\:=\:\:\mathrm{72} \\ $$$$\mathrm{2}^{\mathrm{y}} \:\:+\:\:\mathrm{3}^{\mathrm{x}\:\:} =\:\:\mathrm{108} \\ $$$$\mathrm{Please}\:\mathrm{am}\:\mathrm{not}\:\mathrm{getting}\:\mathrm{correct}\:\mathrm{answer}\:\mathrm{for} \\ $$$$\mathrm{this}\:\mathrm{question}\:\mathrm{using}\:\mathrm{a}\:\mathrm{method}\:\mathrm{proposed}\:. \\ $$
Commented by john santu last updated on 05/May/20
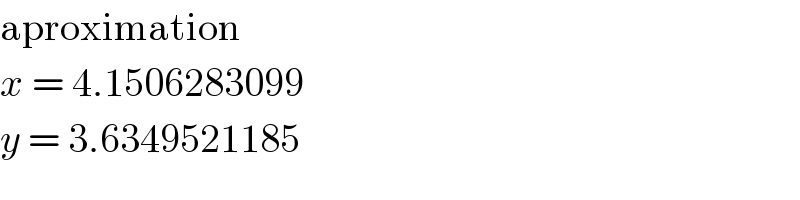
$$\mathrm{aproximation}\: \\ $$$${x}\:=\:\mathrm{4}.\mathrm{1506283099} \\ $$$${y}\:=\:\mathrm{3}.\mathrm{6349521185} \\ $$
Commented by I want to learn more last updated on 05/May/20
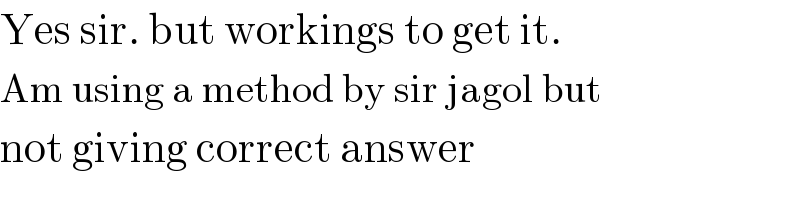
$$\mathrm{Yes}\:\mathrm{sir}.\:\mathrm{but}\:\mathrm{workings}\:\mathrm{to}\:\mathrm{get}\:\mathrm{it}. \\ $$$$\mathrm{Am}\:\mathrm{using}\:\mathrm{a}\:\mathrm{method}\:\mathrm{by}\:\mathrm{sir}\:\mathrm{jagol}\:\mathrm{but} \\ $$$$\mathrm{not}\:\mathrm{giving}\:\mathrm{correct}\:\mathrm{answer} \\ $$
Commented by MJS last updated on 05/May/20

$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{possible}\:\mathrm{path},\:\mathrm{you}\:\mathrm{can}\:\mathrm{only} \\ $$$$\mathrm{approximate} \\ $$$$\mathrm{2}^{{x}} +\mathrm{3}^{{y}} =\mathrm{72}\:\Rightarrow\:{y}=\frac{\mathrm{ln}\:\left(\mathrm{72}−\mathrm{2}^{{x}} \right)}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\mathrm{2}^{{y}} +\mathrm{3}^{{x}} =\mathrm{108}\:\Rightarrow\:{y}=\frac{\mathrm{ln}\:\left(\mathrm{108}−\mathrm{3}^{{x}} \right)}{\mathrm{ln}\:\mathrm{2}} \\ $$$$\mathrm{72}−\mathrm{2}^{{x}} >\mathrm{0}\:\wedge\mathrm{108}−\mathrm{3}^{{x}} >\mathrm{0}\:\Leftrightarrow\:{x}<\frac{\mathrm{ln}\:\mathrm{108}}{\mathrm{ln}\:\mathrm{3}}\approx\mathrm{4}.\mathrm{262} \\ $$$$\frac{\mathrm{ln}\:\left(\mathrm{72}−\mathrm{2}^{{x}} \right)}{\mathrm{ln}\:\mathrm{3}}=\frac{\mathrm{ln}\:\left(\mathrm{108}−\mathrm{3}^{{x}} \right)}{\mathrm{ln}\:\mathrm{2}} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{a}\:\mathrm{calculator} \\ $$
Commented by MJS last updated on 05/May/20
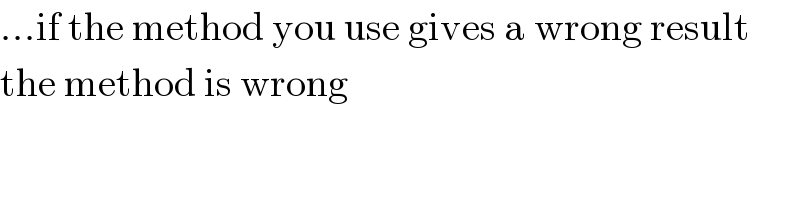
$$...\mathrm{if}\:\mathrm{the}\:\mathrm{method}\:\mathrm{you}\:\mathrm{use}\:\mathrm{gives}\:\mathrm{a}\:\mathrm{wrong}\:\mathrm{result} \\ $$$$\mathrm{the}\:\mathrm{method}\:\mathrm{is}\:\mathrm{wrong} \\ $$
