
Question Number 92118 by otchereabdullai@gmail.com last updated on 04/May/20
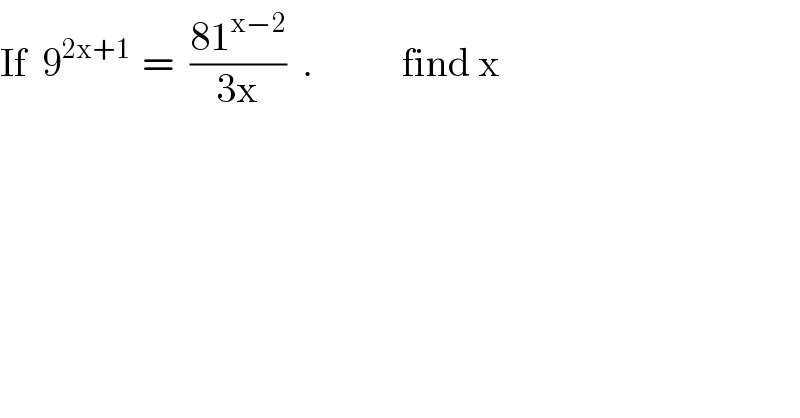
$$\mathrm{If}\:\:\mathrm{9}^{\mathrm{2x}+\mathrm{1}\:\:\:} =\:\:\frac{\mathrm{81}^{\mathrm{x}−\mathrm{2}} }{\mathrm{3x}}\:\:.\:\:\:\:\:\:\:\:\:\:\:\mathrm{find}\:\mathrm{x} \\ $$
Commented by john santu last updated on 05/May/20

$$\mathrm{9}^{\mathrm{2x}+\mathrm{1}} \:=\:\frac{\mathrm{81}^{\mathrm{x}−\mathrm{2}} }{\mathrm{3}^{\mathrm{x}} }\:?? \\ $$
Commented by john santu last updated on 05/May/20

$$\mathrm{x}=\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{11}} } \\ $$
Commented by jagoll last updated on 05/May/20
5.645 029 269 476 76*10^−6
Answered by niroj last updated on 05/May/20
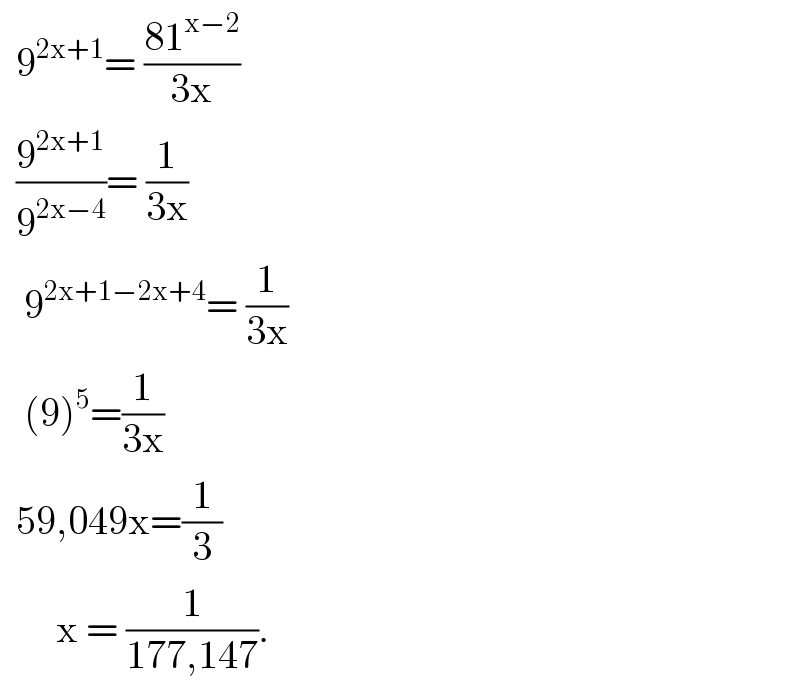
$$\:\:\mathrm{9}^{\mathrm{2x}+\mathrm{1}} =\:\frac{\mathrm{81}^{\mathrm{x}−\mathrm{2}} }{\mathrm{3x}} \\ $$$$\:\:\frac{\mathrm{9}^{\mathrm{2x}+\mathrm{1}} }{\mathrm{9}^{\mathrm{2x}−\mathrm{4}} }=\:\frac{\mathrm{1}}{\mathrm{3x}} \\ $$$$\:\:\:\mathrm{9}^{\mathrm{2x}+\mathrm{1}−\mathrm{2x}+\mathrm{4}} =\:\frac{\mathrm{1}}{\mathrm{3x}} \\ $$$$\:\:\:\left(\mathrm{9}\right)^{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{3x}} \\ $$$$\:\:\mathrm{59},\mathrm{049x}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{177},\mathrm{147}}. \\ $$
Commented by otchereabdullai@gmail.com last updated on 05/May/20

$$\mathrm{fantastic}\:\mathrm{sir}! \\ $$
Commented by niroj last updated on 05/May/20
����
