
Question Number 91771 by M±th+et+s last updated on 03/May/20
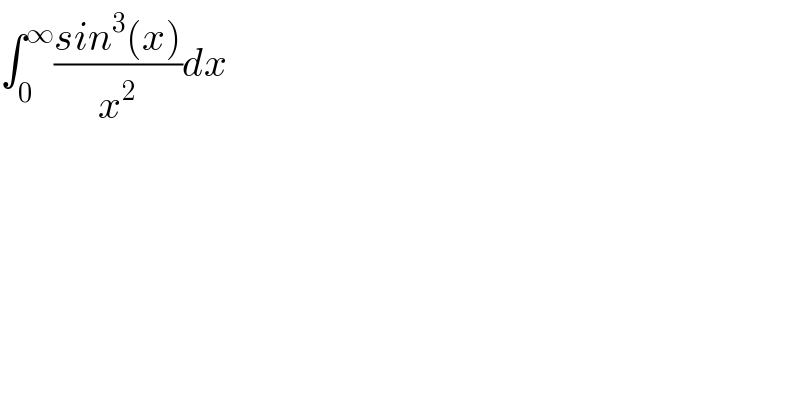
$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{3}} \left({x}\right)}{{x}^{\mathrm{2}} }{dx} \\ $$
Commented by abdomathmax last updated on 03/May/20
![let I=∫_0 ^∞ ((sin^3 (x))/x^2 )dx we hsve by parts I =[−(1/x)sin^3 x]_0 ^∞ +∫_0 ^∞ (1/x)3sin^2 x cosx dx =3 ∫_0 ^∞ ((sin^2 x cosx)/x)dx =(3/2) ∫_0 ^∞ ((cosx sin(2x))/x)dx we have cosx sin(2x)=cosx cos((π/2)−2x) =(1/2){ cos(−x+(π/2))+cosx(3x−(π/2))} =(1/2){sinx +sin(3x)} ⇒ I =(3/4)∫_0 ^∞ ((sinx +sin(3x))/x)dx =(3/4)∫_0 ^∞ ((sinx)/x)dx +(3/4)∫_0 ^∞ ((sin(3x))/x)dx but ∫_0 ^∞ ((sinx)/x)dx =(π/2) ∫_0 ^∞ ((sin(3x))/x)dx =_(3x=t) ∫_0 ^∞ ((sint)/(t/3))×(dt/3) =∫_0 ^∞ ((sint)/t)dt =(π/2) ⇒I =(3/4)(π/2) +(3/4)(π/2) =((3π)/8)+((3π)/8) =2×((3π)/8) =((3π)/4) ⇒I =((3π)/4)](Q91776.png)
$${let}\:{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{3}} \left({x}\right)}{{x}^{\mathrm{2}} }{dx}\:\:{we}\:{hsve}\:{by}\:{parts} \\ $$$${I}\:=\left[−\frac{\mathrm{1}}{{x}}{sin}^{\mathrm{3}} {x}\right]_{\mathrm{0}} ^{\infty} \:+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{x}}\mathrm{3}{sin}^{\mathrm{2}} {x}\:{cosx}\:{dx} \\ $$$$=\mathrm{3}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} {x}\:{cosx}}{{x}}{dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cosx}\:{sin}\left(\mathrm{2}{x}\right)}{{x}}{dx}\:{we}\:{have} \\ $$$${cosx}\:{sin}\left(\mathrm{2}{x}\right)={cosx}\:{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:{cos}\left(−{x}+\frac{\pi}{\mathrm{2}}\right)+{cosx}\left(\mathrm{3}{x}−\frac{\pi}{\mathrm{2}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{sinx}\:+{sin}\left(\mathrm{3}{x}\right)\right\}\:\Rightarrow \\ $$$${I}\:\:=\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{sinx}\:+{sin}\left(\mathrm{3}{x}\right)}{{x}}{dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{{sinx}}{{x}}{dx}\:+\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}\left(\mathrm{3}{x}\right)}{{x}}{dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{sinx}}{{x}}{dx}\:=\frac{\pi}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}\left(\mathrm{3}{x}\right)}{{x}}{dx}\:=_{\mathrm{3}{x}={t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sint}}{\frac{{t}}{\mathrm{3}}}×\frac{{dt}}{\mathrm{3}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{sint}}{{t}}{dt}\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow{I}\:=\frac{\mathrm{3}}{\mathrm{4}}\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{4}}\frac{\pi}{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}\pi}{\mathrm{8}}+\frac{\mathrm{3}\pi}{\mathrm{8}}\:=\mathrm{2}×\frac{\mathrm{3}\pi}{\mathrm{8}}\:=\frac{\mathrm{3}\pi}{\mathrm{4}}\:\Rightarrow{I}\:=\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$
