
Previous in Differential Equation Next in Differential Equation
Question Number 91750 by jagoll last updated on 02/May/20
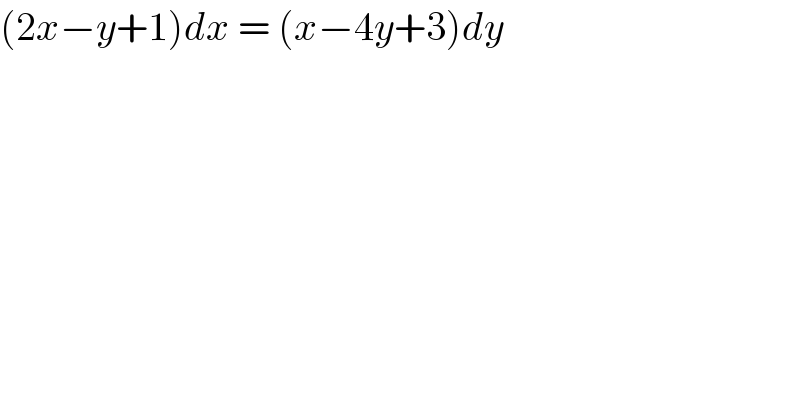
$$\left(\mathrm{2}{x}−{y}+\mathrm{1}\right){dx}\:=\:\left({x}−\mathrm{4}{y}+\mathrm{3}\right){dy} \\ $$
Commented by mr W last updated on 02/May/20

$${see}\:{Q}\mathrm{90770} \\ $$
Commented by john santu last updated on 03/May/20
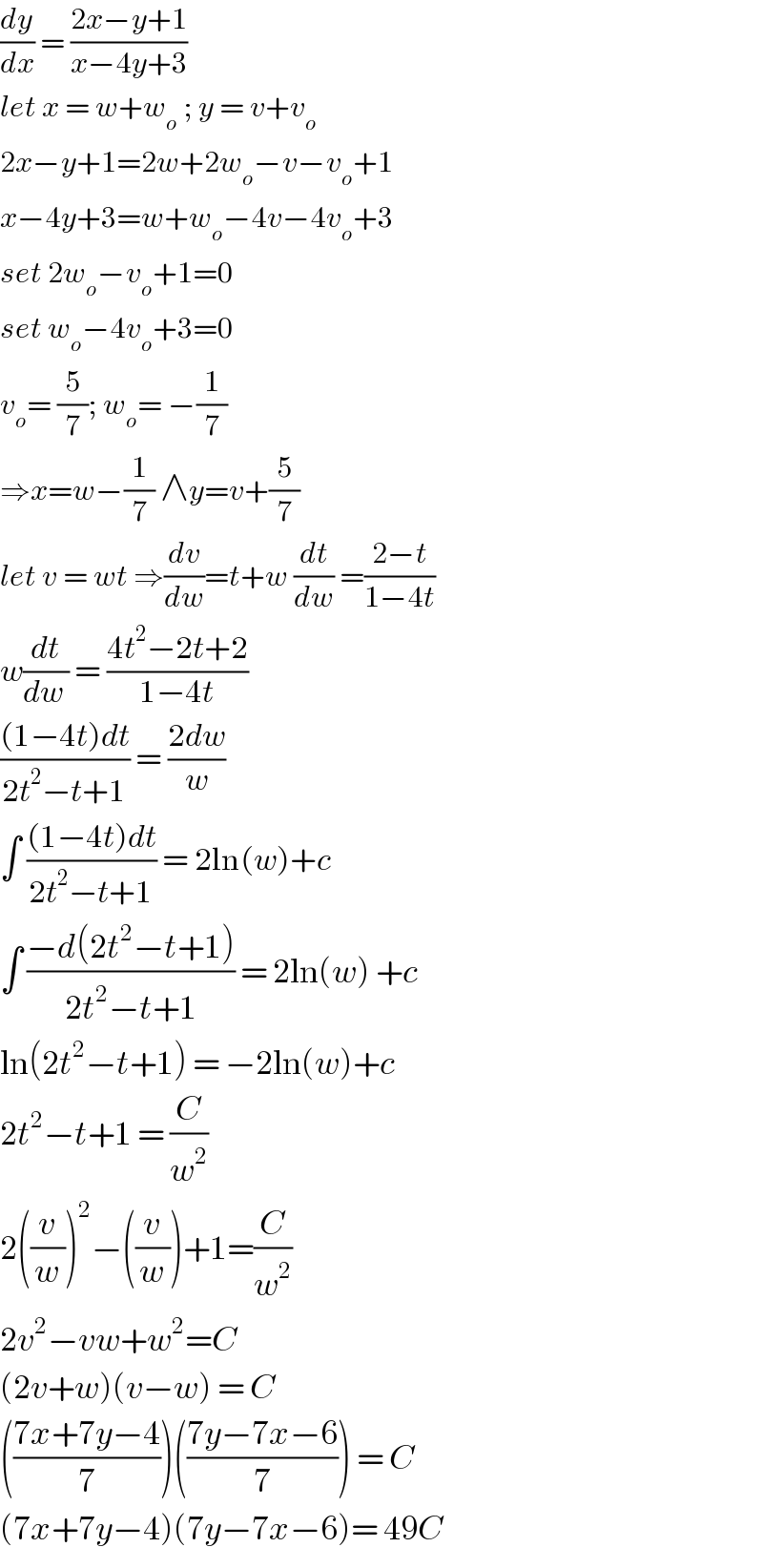
$$\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{2}{x}−{y}+\mathrm{1}}{{x}−\mathrm{4}{y}+\mathrm{3}} \\ $$$${let}\:{x}\:=\:{w}+{w}_{{o}} \:;\:{y}\:=\:{v}+{v}_{{o}} \\ $$$$\mathrm{2}{x}−{y}+\mathrm{1}=\mathrm{2}{w}+\mathrm{2}{w}_{{o}} −{v}−{v}_{{o}} +\mathrm{1} \\ $$$${x}−\mathrm{4}{y}+\mathrm{3}={w}+{w}_{{o}} −\mathrm{4}{v}−\mathrm{4}{v}_{{o}} +\mathrm{3} \\ $$$${set}\:\mathrm{2}{w}_{{o}} −{v}_{{o}} +\mathrm{1}=\mathrm{0} \\ $$$${set}\:{w}_{{o}} −\mathrm{4}{v}_{{o}} +\mathrm{3}=\mathrm{0} \\ $$$${v}_{{o}} =\:\frac{\mathrm{5}}{\mathrm{7}};\:{w}_{{o}} =\:−\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\Rightarrow{x}={w}−\frac{\mathrm{1}}{\mathrm{7}}\:\wedge{y}={v}+\frac{\mathrm{5}}{\mathrm{7}} \\ $$$${let}\:{v}\:=\:{wt}\:\Rightarrow\frac{{dv}}{{dw}}={t}+{w}\:\frac{{dt}}{{dw}}\:=\frac{\mathrm{2}−{t}}{\mathrm{1}−\mathrm{4}{t}} \\ $$$${w}\frac{{dt}}{{dw}\:}\:=\:\frac{\mathrm{4}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{2}}{\mathrm{1}−\mathrm{4}{t}} \\ $$$$\frac{\left(\mathrm{1}−\mathrm{4}{t}\right){dt}}{\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}}\:=\:\frac{\mathrm{2}{dw}}{{w}} \\ $$$$\int\:\frac{\left(\mathrm{1}−\mathrm{4}{t}\right){dt}}{\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}}\:=\:\mathrm{2ln}\left({w}\right)+{c} \\ $$$$\int\:\frac{−{d}\left(\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}\right)}{\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}}\:=\:\mathrm{2ln}\left({w}\right)\:+{c} \\ $$$$\mathrm{ln}\left(\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}\right)\:=\:−\mathrm{2ln}\left({w}\right)+{c} \\ $$$$\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}\:=\:\frac{{C}}{{w}^{\mathrm{2}} } \\ $$$$\mathrm{2}\left(\frac{{v}}{{w}}\right)^{\mathrm{2}} −\left(\frac{{v}}{{w}}\right)+\mathrm{1}=\frac{{C}}{{w}^{\mathrm{2}} } \\ $$$$\mathrm{2}{v}^{\mathrm{2}} −{vw}+{w}^{\mathrm{2}} ={C} \\ $$$$\left(\mathrm{2}{v}+{w}\right)\left({v}−{w}\right)\:=\:{C} \\ $$$$\left(\frac{\mathrm{7}{x}+\mathrm{7}{y}−\mathrm{4}}{\mathrm{7}}\right)\left(\frac{\mathrm{7}{y}−\mathrm{7}{x}−\mathrm{6}}{\mathrm{7}}\right)\:=\:{C} \\ $$$$\left(\mathrm{7}{x}+\mathrm{7}{y}−\mathrm{4}\right)\left(\mathrm{7}{y}−\mathrm{7}{x}−\mathrm{6}\right)=\:\mathrm{49}{C} \\ $$
