
Question Number 91036 by niroj last updated on 27/Apr/20
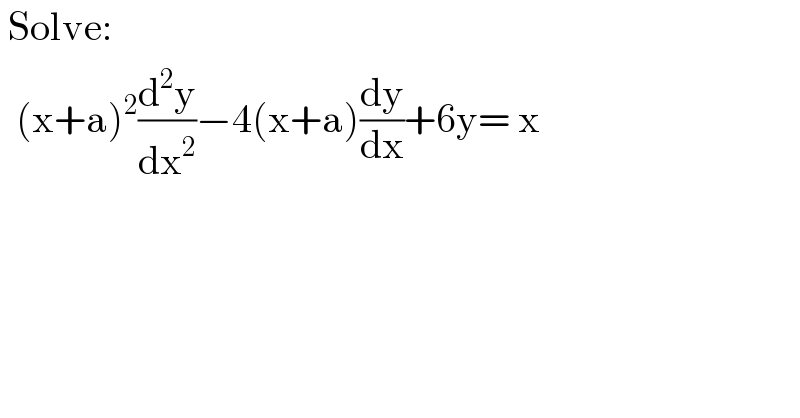
$$\:\mathrm{Solve}: \\ $$$$\:\:\left(\mathrm{x}+\mathrm{a}\right)^{\mathrm{2}} \frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }−\mathrm{4}\left(\mathrm{x}+\mathrm{a}\right)\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{6y}=\:\mathrm{x} \\ $$
Answered by MWSuSon last updated on 27/Apr/20

$${let}\:{x}+{a}={e}^{{z}} \:\Rightarrow{x}={e}^{{z}} −{a} \\ $$$$\left({x}+{a}\right)^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={D}\left({D}−\mathrm{1}\right){y} \\ $$$$\left({x}+{a}\right)\frac{{dy}}{{dx}}={Dy} \\ $$$${D}\left({D}−\mathrm{1}\right){y}−\mathrm{4}{Dy}+\mathrm{6}{y}={e}^{{z}} −{a} \\ $$$$\left({D}^{\mathrm{2}} −{D}−\mathrm{4}{D}+\mathrm{6}\right){y}={e}^{{z}} −{a} \\ $$$$\left({D}^{\mathrm{2}} −\mathrm{5}{D}+\mathrm{6}\right){y}={e}^{{z}} −{a} \\ $$$${Auxillary}\:{eauation} \\ $$$${m}^{\mathrm{2}} −\mathrm{5}{m}+\mathrm{6}=\mathrm{0} \\ $$$$\left({m}−\mathrm{2}\right)\left({m}−\mathrm{3}\right)=\mathrm{0} \\ $$$${m}=\mathrm{2},\mathrm{3} \\ $$$${y}_{{c}} ={C}_{\mathrm{1}} {e}^{\mathrm{2}{z}} +{C}_{\mathrm{2}} {e}^{\mathrm{3}{z}} \\ $$$${y}_{{p}} =\frac{\mathrm{1}}{{D}^{\mathrm{2}} −\mathrm{5}{D}+\mathrm{6}}\left({e}^{{z}} −{a}\right) \\ $$$$=\frac{\mathrm{1}}{{D}^{\mathrm{2}} −\mathrm{5}{D}+\mathrm{6}}{e}^{{z}} −\frac{\mathrm{1}}{{D}^{\mathrm{2}} −\mathrm{5}{D}+\mathrm{6}}{a} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{5}+\mathrm{6}}{e}^{{z}} −{a}\frac{\mathrm{1}}{{D}^{\mathrm{2}} −\mathrm{5}{D}+\mathrm{6}}{e}^{\mathrm{0}{x}} \\ $$$$=\frac{{e}^{{z}} }{\mathrm{2}}−{a}\frac{\mathrm{1}}{\mathrm{0}−\mathrm{0}+\mathrm{6}}{e}^{\mathrm{0}{x}} \\ $$$$=\frac{{e}^{{z}} }{\mathrm{2}}−\frac{{a}}{\mathrm{6}} \\ $$$${y}={C}_{\mathrm{1}} {e}^{\mathrm{2}{z}} +{C}_{\mathrm{2}} {e}^{\mathrm{3}{z}} +\frac{{e}^{{z}} }{\mathrm{2}}−\frac{{a}}{\mathrm{6}} \\ $$$${but}\:{x}+{a}={e}^{{z}} \Rightarrow{z}={log}_{{e}} \left({x}+{a}\right) \\ $$$${y}={C}_{\mathrm{1}} \left({x}+{a}\right)^{\mathrm{2}} +{C}_{\mathrm{2}} \left({x}+{a}\right)^{\mathrm{3}} +\frac{\left({x}+{a}\right)}{\mathrm{2}}+\frac{{a}}{\mathrm{6}} \\ $$
Commented by peter frank last updated on 27/Apr/20

$${thank}\:{you} \\ $$
Commented by peter frank last updated on 27/Apr/20

$${thank}\:{you} \\ $$
Commented by niroj last updated on 03/May/20
��
